Inscription / Connexion Nouveau Sujet
Circuit électronique
 philou28
philou28Bonsoir
J'ai un problème sur ce circuit :
Le gain de l'amplificateur de tension est de 2.
Comment établir l'équation différentielle reliant s et e ?
merci beaucoup pour l'aide.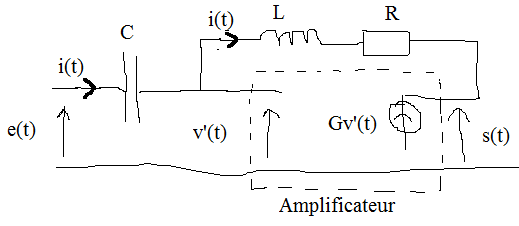
***Edit gbm : image recardée***
Bonsoir
Le plus simple consiste sans doute à établir l'équation différentielle dans le cas particulier du régime sinusoïdal établi puis à généraliser.
De façon immédiate, le théorème de Millman conduit à :
Après simplification, sauf étourderie de ma part, cela donne :
Sinon, à peine plus long, tu peux écrire que l'association série C,R,L se comporte en diviseur de tension vis à vis de la tension (e-s) :
On obtient le même résultat après simplification.
Ensuite, on démontre qu'en régime sinusoïdal, multiplier le complexe associé à une tension par (j )n est équivalent à prendre la dérivée nième de cette tension. Ainsi, par exemple :
)n est équivalent à prendre la dérivée nième de cette tension. Ainsi, par exemple :
- au complexe jRC .s correspond
.s correspond
-au complexe -LC 2.e correspond
2.e correspond
On admet que l'équation différentielle obtenue par cette méthode est aussi valide en régime variable quelconque.
Dans votre application de millman je comprend la première expression de v' mais après je ne comprend pas. Désolé.
Merci j'ai grâce à vous l'équation différentielle.
Comment étudier la stabilité par le régime libre ?
Merci
Bonjour
D'abord un complément à mon message précédent. J'ai tenu à te présenter la méthode utilisant les complexes en régime sinusoïdal car c'est la seule qui sera efficace avec des circuits compliqués. Ici, il s'agit d'un simple circuit RLC série ; la méthode directe peut s'appliquer. Je te l'expose rapidement; à toi ensuite de choisir...
Si q désigne la charge de l'armature gauche du condensateur, on peut écrire :
La tension aux bornes de l'ensemble {L,R} peut s'écrire :
Après simplification, on obtient bien sûr la même équation différentielle.
Comment étudier la stabilité par le régime libre ?
L'équation différentielle vérifiée par s(t) peut s'écrire sous la forme :
où
 et
et  sont des constantes dépendant de R, L, C et G. f est une fonction de la dérivée première de e et de sa dérivée seconde par rapport au temps.
sont des constantes dépendant de R, L, C et G. f est une fonction de la dérivée première de e et de sa dérivée seconde par rapport au temps.
La solution générale de cette équation différentielle est une somme de deux termes :
1° un premier terme sh(t) solution de l'équation avec second terme nul :
Il faut chercher les solutions de la forme générale :
Cela va te conduire à écrire l'équation caractéristique dont r est solution. Pour que le circuit soit stable, les valeurs possibles de r doivent être telles que sh(t) tende vers zéro. Si sh(t) tend vers l'infini : le circuit est instable ; en pratique s tend vers une valeur imposée par la saturation de l'amplificateur.
2° le second terme dépend de e(t). Sa la tension d'entrée est périodique, ce second terme est une fonction périodique de même fréquence que e(t).
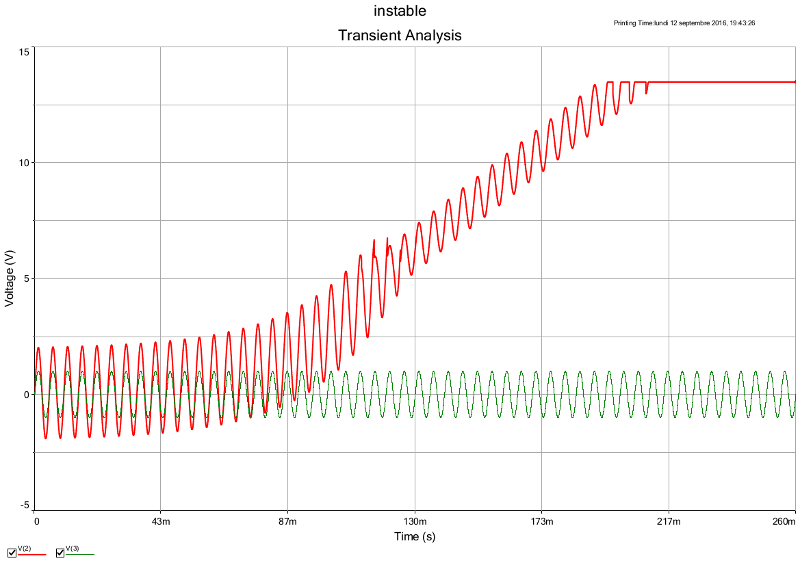
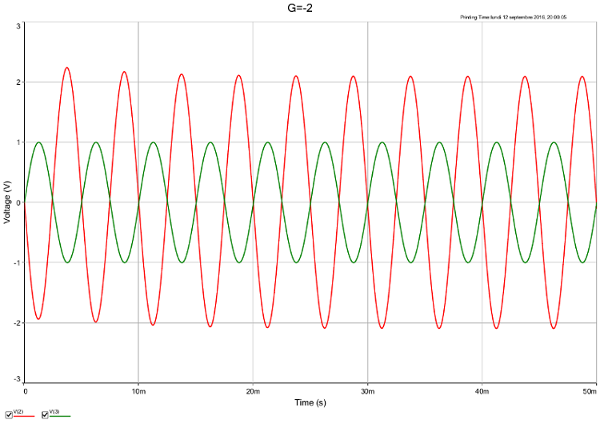
Pour illustrer mon propos précédent, voici une simulation avec G=2 puis une autre avec G=-2 pour une tension d'entrée sinusoïdale de fréquence 200Hz et d'amplitude 1V. Par ailleurs, j'ai choisi :
Tu devrais arriver à montrer que la stabilité dépend du signe de  (voir message précédent) donc du signe de (G-1).
(voir message précédent) donc du signe de (G-1).
Pour G= 2 : la tension de sortie dérive vers la tension de saturation de l'amplificateur. Pour G=-2 la tension de sortie subit quelques fluctuations d'amplitude puis se stabilise (je n'ai représenté que le début de l'enregistrement pour plus de visibilité)
en vert : e(t) ; en route : s(t)
Merci pour ces détails mais je ne comprend pas : Pour que le circuit soit stable, les valeurs possibles de r doivent être telles que sh(t) tende vers zéro. Si sh(t) tend vers l'infini : le circuit est instable ; en pratique s tend vers une valeur imposée par la saturation de l'amplificateur.
La solution homogène sans second membre, je trouve :
 >0 sh(t)=Aexp(-
>0 sh(t)=Aexp(- +
+ (
( 2-
2- ))
))
si 
 =0 sh(t)=(A+Bt)exp(-
=0 sh(t)=(A+Bt)exp(- )
)
si  <0 sh(t)=exp(-
<0 sh(t)=exp(- t)(Aexp(i
t)(Aexp(i (
( -
- 2))+Bexp(i
2))+Bexp(i (
( )-
)- 2)))
2)))
Par contre je ne sais pas faire avec le second membre.
En fait mon exercice il y a ces 4 question dans cet ordre :
1 établir l'équa diff reliant s et e ça c'est fait
2 Etudier la stabilité par le régime libre
3 donner la forme matématiques de s(t) j'ai trouvé sh(t) mais pas avec le second membre
4 que se passe t il si une légère perturbation écarte la sortie de son régime établi? s dérive vers la tension de saturation de l'ampli
Merci
Bonsoir
Il s'agit d'étudier le régime libre... Pas très clair... par analogie avec le régime libre d'un oscillateur mécanique, il s'agit peut-être d'étudier la réponse à un échelon de tension. Le condensateur étant initialement déchargé en absence de courant, la tension e passe à la date t=0 de la valeur nulle à une valeur constante E. Cela va te ramener à étudier l'équation différentielle avec second terme nul comme tu as commencé à le faire mais tu as commis des erreurs dans les expressions des racines de l'équation caractéristique.  est positif mais le signe de
est positif mais le signe de  dépend de la valeur de G...
dépend de la valeur de G...
Bonjour
L'équa. dif. que tu as dû obtenir s'écrit dans le cas général :
Soit, en divisant tous les termes par (LC) et en utilisant les notations définies dans un message précédent :
Je t'ai présenté déjà l'étude de la stabilité en imaginant e(t) comme une tension sinusoïdale. Maintenant que tu as fourni un énoncé plus complet, je constate que ce n'est pas l'approche choisi ici. Cet énoncé, tel que tu l'as écrit me parait tout de même très vague : le schéma et la première question évoque clairement l'existence d'une tension d'entrée e(t) puis apparemment, plus rien n'est dit sur cette tension... On peut imaginer de partir d'un état où i=0, s=0,e=0 le condensateur étant déchargé. A t = 0, la tension e passe très rapidement (en une durée de l'ordre de quelques microsecondes) de la valeur e= 0 à une valeur constante E non nulle. Pendant cette durée très courte, de/dt prend une valeur élevée, ce qui crée un courant dans la branche RLC puis ensuite, e(t) devenant constante, s(t) est solution de l'équation précédente avec second membre nul. On dit que le circuit est soumis à un échelon de tension. Sachant que : G = 2, cela donne :
Attention : tu as cherché à résoudre cette équation avec alors que cette valeur est ici négative. L'équation caractéristique s'écrit :
Les deux racines de cette équations sont réelles, l'une est strictement positive, l'autre strictement négative :
La solution recherchée a pour expression générale :
Le fait que r1 soit strictement positif avec A non nul fait que, théoriquement, s(t) tend vers + ou - l'infini, selon le signe de A. En pratique, la tension de sortie va dériver vers Vsat ou -Vsat, les tensions de saturation de l'amplificateur.
Je ne pense pas que la détermination des valeurs de A et B soit demandée ici.
Une autre approche est celle évoquée dans la dernière question. On cherche à étudier la stabilité de l'état e = 0, s= 0. Cela suppose court-circuitée l'entrée. On suppose alors que les défauts de l'amplificateur et/ou les effets d'antenne dans le circuit, génère à une date t = 0 une très faible tension parasite. On est ainsi amené à résoudre la même équation différentielle avec second membre nul que précédemment : si la solution tend théoriquement vers l'infini : l'état s = 0 sera considéré comme instable, s(t) tend comme précédemment vers Vsat ou -Vsat en fonction des caractéristiques de cette tension parasite. En revanche, si la solution s(t) à l'équation tend vers zéro, l'état s= 0 pourra être considéré comme stable, s restant toujours très proche de zéro quels que soit les défauts, a priori faibles de l'ampli.
Remarque : supposons . On obtient alors
. Cela conduit à l'étude que tu as commencé dans ton message du 13/9 à 0h14 : Dans les trois cas étudiés, s(t) tend vers zéro. L'état s= 0 est stable.
Tout cela bien sûr sous réserve, compte tenu de l'imprécision de l'énoncé...
Je ne pense pas que la détermination des valeurs de A et B soit demandée ici.
Au cas où...
Reprends les équations générales écrites dans mon message du 12-09-16 à 15:27 en les adaptant à la date t = 0+ :
Le condensateur impose la conservation de la tension à ses bornes :
(q/C) a même valeur (ici 0) à t=0- et à t=0+
A t=0+ : s =G.e=G.E
La bobine impose la continuité de l'intensité dans sa branche : i a la même valeur (ici 0) à t=0- et à t=0+ :
à t=0+ :
Ces deux conditions sur s permettent la détermination des constantes A et B.
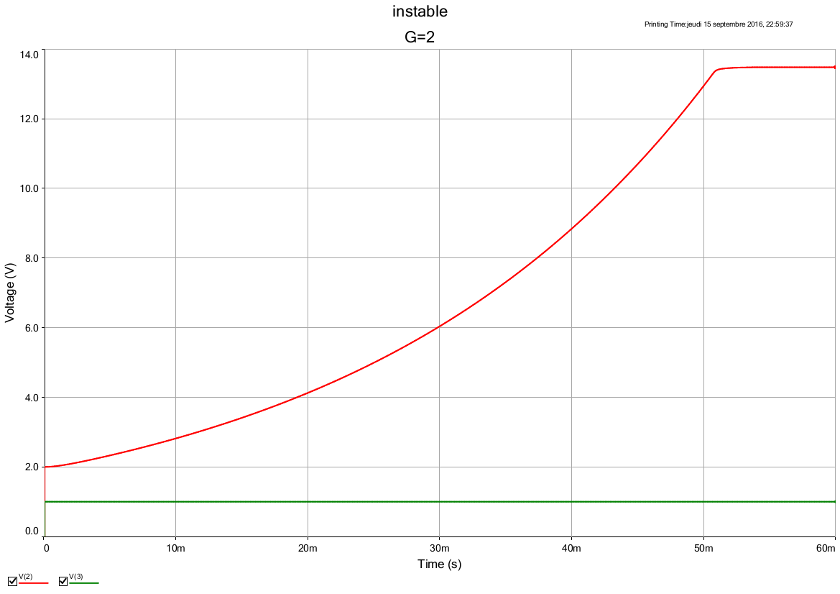
Voici pour illustrer mes propos précédents les simulations correspondant à un échelon de tension correspondant à E = 1V. Les valeurs de R,L et C correspondent aux valeurs de mon message du 12-09-16 à 20:18.
La première simulation correspond à G = 2 : s(t) dérive vers Vsat (13,5V environ).
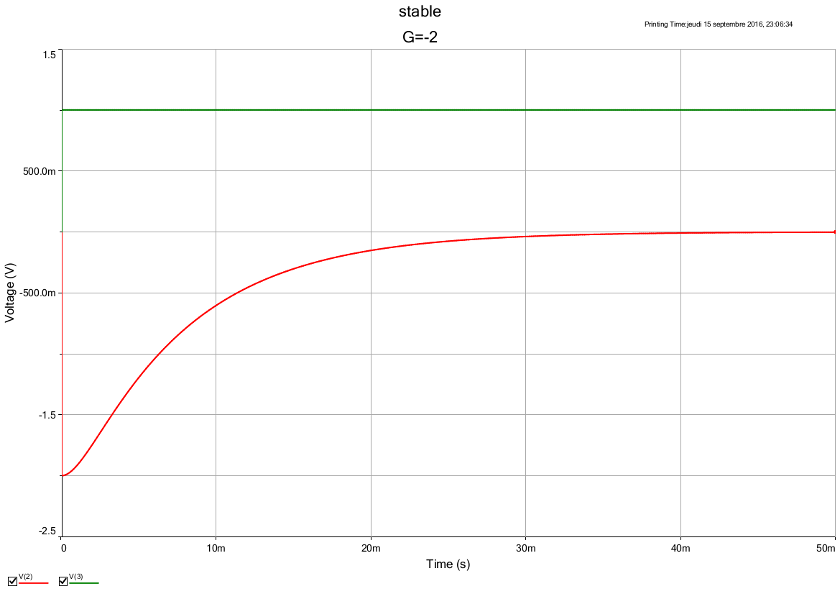
La seconde correspond à G = -2 : s(t) tend vers zéro.
Dans les deux cas, les courbes s(t) correspondent bien aux conditions initiales données dans mon message précédent.