Inscription / Connexion Nouveau Sujet
Circuit de Wien
Bonjour,mon professeur m'a donné ce circuit à étudier:

Mais j'aurai besoin d'aide pour démarrer.
Dans l'énoncé ils disent :
Soit le circuit suivant ou l'on ferme l'interrupteur à t=0(C est un condensateur initialement chargé,v=v_0 à t=0,et C' est initialement déchargé).
a)Montrer que u(t) est la solution d'une équation différentiel du second ordre à coefficient constants avec second membre nul.
Et pour l'instant j'ai pu dire cela:
Le condensateur C' est initialement déchargé donc il se comporte comme un récepteur.
Par conséquent le courant et la tension sont en sens inverse.
On sait aussi que si C' est décharger,la tension(au borne de C') est nulle mais pas le courant.
On peut aussi dire qu'il n'y a plus de courant dans C vu que C est chargé.
Après je me demande si la tension en C' est bien nulle ou si c'est pas v(t) comme dans mon schéma(pas sûr qu'il soit bon).
Mon schéma:
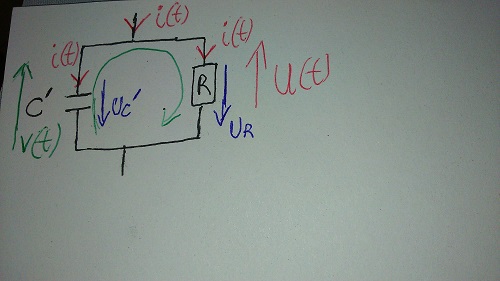
Bonsoir,
La méthode la plus rapide est la suivante :
- elle consiste dans un premier temps à étudier le circuit en régime sinusoïdal forcé en utilisant les complexes ;
- ensuite on retrouve l'équation différentielle sachant qu'une multiplication par (jw)n du complexe associé à une grandeur instantanée est équivalente à une dérivée nième de la valeur instantanée.
Sinon, la loi des mailles et la loi des nœuds directement appliquées aux grandeurs instantanées est possible quoique moins rapide.
Merci pour votre réponse 
J'aurai bien utilisé les nombres complexes,mais on ne les a pas encore vu avec mon prof(même si je connais les bases ).
Donc je vais tenter d'utiliser la loi des maille c'est ça seulement qu'on a vu avec la loi des noeuds.
Quelques pistes :
Tu te débarrasses de la primitive en dérivant par rapport au temps.
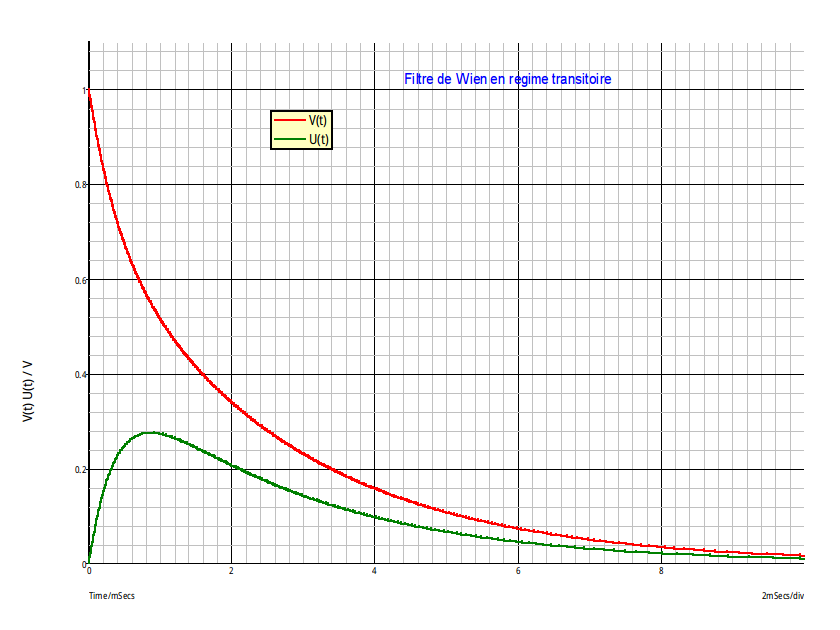
Voici une simulation qui pourra peut-être t'aider. Elle correspond à :
C = C' = 100nF ; R = 10k ; V(0) = 1V
; V(0) = 1V
Toutes mes excuses : j'ai commis une faute de signe dans mon message précédent : une intensité positive correspond à une décharge du condensateur de gauche. Il faut lire à la seconde ligne :


