bonsoir,

1) c'est du cours: mouvement à force central - équations de Binet

cf

Mais si on suppose qu'on est en cinématique où la notion de force n'intervient pas, est ce qu'on peut parler de force

1) pour la trajectoire plane: tu démontres que d/dt(OM ^ V) = 0
ensuite tu utilises les formules de Binet

J'arrive pas à démontrer ce résultat je dois poser OM =rer ou bien

sais-tu dériver un produit vectoriel ?

d(A^B)/dt = dA/dt ^ B + A ^ dB/dt

donc d/dt(OM ^ V) = d/dt(OM) ^ V + ...

A, B, OM, V étant ici des vecteurs

d/dt(OM ^ V)= V ^ V + OM ^ γ =0 car V et V sont colinéaire de même OM et γ  
Mais que représente le produit vectoriel OM ^ V

normalement, on démontre que _O (moment cinétique par rapport à O) est constant,

_O = OM ^ mV

et on en déduit que V est tjs orthogonal à _O qui est fixe donc que le mvt est plan

mais si tu ne veux pas évoquer les notions usuelles de mécanique, tu arrives au meme résultat en démontrant que R = OM ^ V est fixe
donc que le mvt est plan

OK MERCI BEAUCOUP, pour la nature de la trajectoire j'ai compris comment l'obtenir à partir du formule de Binet mais on a utilisé RFD et la aussi je ne peux pas introduire la notion de force y a t-il autre solution?

a) tu démontres d'abord la loi des aires en écrivant que l'accélération tangentielle est nulle: r²' = C
b) tu démontres ensuite les formules de Binet qui exprime V et en fonction de u() = 1/r
cf

tu en déduis l'équation de la trajectoire

(ce ne sont que des résultats de cinématique si je ne m'abuse)

Bonsoir

Pour démontrer que le mvt est plan

OM ⃗ ⃗ = 0⃗  (O origine du repère; M le point matériel en question, produit vectoriel)

ceci parce que OM⃗ et ⃗ sont par hypothèse dans le mêm plan

Par ailleurs

d(OM⃗ v⃗)/dt = v⃗v⃗  + OM⃗ ⃗ (propiété produit vectoriel)

donc d(OM⃗ v⃗)/dt = 0⃗, OM⃗ v⃗ est constant, en particulier en direction

ur⃗ et v⃗ restent dans le même plan à chaque instant ...

Le temps de batailler avec l"éditeur et les choses ont bien avancé ... de quoi je me mêle, je me demande ...

Pour l'équation de la trajectoire on aura x²/a²+y²/b²=1 mais comment faire pour pour obtenir a et b en fonction de p et e

Euh ...

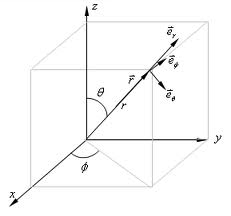
Tu dois connaître ou avoir un formulaire pour passer des coordonnées sphériques aux coordonnées cartésiennes:

Dans le cas présent, tu peux fixer = 0 (mvt plan)

Alors OM⃗  = r.ur⃗  = r(cos.k⃗  + sin.i⃗ )  (=0, plan = xOz)

Tu connais r ... donc tu trouves les coordonnées (x,y) de M dans le repère (0,i⃗,k⃗)

Je pense qu'alors a et b t'apparaitront ...

PS: j'en profite pour revenir sur la constante des aires. Lorsque que tu exprimes le produit vectoriel OM⃗v⃗ (dont on a démontré qu'il était constant) en fonction des coordonnées de M (r,,) tu trouves r2 d/dt = Cste

Est ce que vous être plus précis pour le indications:je ne vois pas de piste pour le moment

bonsoir,

dans quel repère cartésien te demande-t-on l'équation de l'ellipse? (quelle origine, quels axes?)

Je pense que l'équation de l'ellipse c'est dans le repère (O,i,j) sinon on ne nous dit pas que l'origine du vecteur position r en coordonnées polaires est situé sur l'un des foyers

Bonjour

Dans un repère cartésien quelconque, les coordonnées sphériques (r,,) sont "conventionnellement" représentées par le petit dessin ci dessous.

Dans l'exercice, dans un repère (O, i⃗,j ⃗,k ⃗), un point M tel que OM ⃗ = r ⃗ suit le mouvement dont l'accélération est donnée, ce qui a permis de décrire également la trajectoire (au passage, pour arriver à l'équation proposée dans l'énoncé, on a fait le choix de fixer =0 à t=0).

On peut même en déduire que O est le foyer de la conique.

Le mouvement étant plan d(u ⃗)/dt = 0 ⃗ on fait le choix de fixer (en faisant tourner si nécessaire le repère cartésien le long de Oz) afin de trouver une équation canonique de la conique.

Ensuite, pour répondre à la question précision de Sami,

OM⃗  = r.ur⃗  = r(cos.k⃗  + sin.i⃗ )

Donc dans le repère (O,i⃗,j⃗,k⃗) les coordonnées (x,y,z) du point M sont:

x = r.sin
y = 0
z = r.cos

Est ce un peu plus clair?

PS: J'oublais ...

A ce stade, l'origine du repère est un foyer. Dans l'équation de type X2/a2 + Y2/b2 ... l'origine est le centre de symétrie. En développant dans l'exercice l'expression x2 + z2 = [p/(1+ecosθ)]2, on sera amené à le faire ...

bonjour,

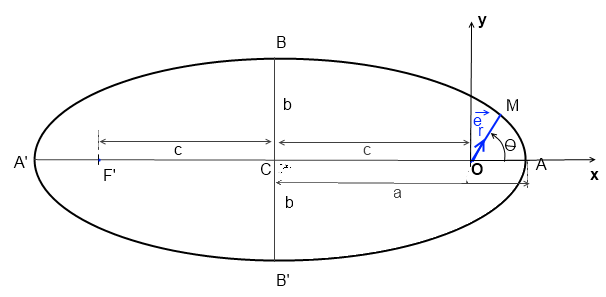
donc le repère cartésien est R(O,x,y), avec O foyer de l'ellipse: (cf figure)

il y a 2 façons de procéder:

a) tu écris que l'ellipse a pour équation: (x+c)² / a² + y²/b² = 1
et tu calcules a, b et c en fct de e et p

b) ou, comme le propose PerArGal, tu pars de l'eq. paramétrique:

x = r cos
y = r sin

et tu élimines


à toi de choisir

@krinn

Mais une question me taraude soudain en regardant ce très beau schéma ...

Question 1:

@PerArGal

c'est vrai qu'on lui a déjà fait redémontrer la loi des aires et les formules de Binet, alors pourquoi pas aussi que r = p/(1+e cosO) est bien l'équation polaire d'une conique
mais bon, on est samedi, c'est le week-end, je propose donc de demander au web de le démontrer:
cf

C'est pas mâché, mais c'est mouliné fin ...

@Sami, à toi de jouer!

Sans aucun "paternalisme" de ma part: je crois important de bien "dominer" cet exercie (un classique en colle) qui fait référence à des théorèmes courants et utilise des outils courants de l'analyse vectorielle, représentation dans l'espace et dérivation ... n'hésite pas à poser des questions et y conscrer du temps pour pouvoir le rejouer de manière "fluide".