Inscription / Connexion Nouveau Sujet
Chimie-Cinetique expérimentale
Bonjour à tous,
Voici l'énoncé : la vapeur d'eau se décompose suivante certaines conditions en H2 et O2 2H2O=2H2+O2
On etudie cette reaction a une temperature T dans un récipient de volume constant. On introduit à l'instant t=0 une quantite de matière n0 de vapeur d'eau et on suit l'évolution de la pression partielle en vapeur d'eau PH2O au cours du temps.
Je bloque depuis plusieurs heures sur une question. Voici la question :
2. En deduire que la pression partielle de l'eau obeit a la reaction : PH2O = PH2O(indice 0) × exp(-2kt) où k est la constante de vitesse et PH2O(indice 0) est la pression initiale de l'eau.
La question précédente :
1. La réaction est d'ordre 1, donner la loi de vitesse de cette réaction.
j'ai trouvé v = k ×[H2O] d'où [H2O]=[H2O]0×exp(-2kt)
Merci pour votre réponse !
Bonjour
Il faut partir de la définition de la pression partielle dans le cas où le mélange gazeux est assimilé à un mélange de gaz parfaits.
où n est la quantité totale de gaz et P la pression totale. La loi des gaz parfait donne :
Je te laisse terminer. Tu devrais facilement démontrer que la pression partielle en vapeur d'eau est proportionnelle à la concentration en vapeur d'eau à T et V fixes.
Ah oui logiquement, suis je bête, je suis allé chercher un peut loin (tableau d'avancement),...
J'ai une autre question sur la quelle je bloque.
t(s) 0 2 4 10 20 30
PH2O (bar) 20.00 18.76 17.61 14.55 10.58 7.70
2. Calculer la constante k de la réaction à la température T.
j'ai un problème d'affichage avec ma calculatrice, donc je ne peut le faire
3. Etablir l'expression du temps de demi-réaction et calculer sa valeur à la température T.
en découle....
4. On donne le temps de demi-réaction τ1 = 1841 s à T1 = 1000K et τ2 = 0.256 s à T2 = 1500K.
j'ai trouvé 221,5kj.mol-1, mais ça me paraît bizarre
Déterminer l'énergie d'activation de la réaction et le facteur préexponentiel (facteur de fréquence)
5. Calculer la température de travail.
je ne sais pas ce que s'est !
Merci pour votre aide !
Pour 1), tu représentes les variations en fonction de t de avec Po : pression partielle initiale en vapeur d'eau. Tu devrais obtenir des points sensiblement alignées sur une droite passant par l'origine dont le coefficient directeur va te permettre d'obtenir k.
Pour 5) : la température de travail est la température à laquelle s'est déroulée l'expérience correspondant au tableau de mesures. Tu as déterminé k, tu peux en déduire T avec la loi d'Arrhénius.
Pour 4) : la valeur du temps de demi réaction est bien 0,256s ?
Je vous pour votre réponse !
Alors c'est à partir de là, que j'ai une multitude de question...
P0 je prends quelle valeur ? Idem pour PH2O ?
La 5, j'ai compris.
La 4, je suppose qu'il faut utiliser la loi d'Arrhénius ? Avec les valeurs de l'ennonce on peut determiner k1 et k2 mais sinon je n'ai aucune idée...
Compte tenu des réponses précédentes :
Tu exploites le tableau de mesures fourni : Po=20bar. Le coefficient directeur de la droite moyenne permet d'obtenir k (attention à l'unité).
Pour 4 : tu écris la loi d'Arrhénius à T1 puis la même loi à T2 : cela te donne deux équations à deux inconnues : l'énergie d'activation et le facteur de fréquence. Tu n'as pas répondu sur le temps de demie réaction à T2.
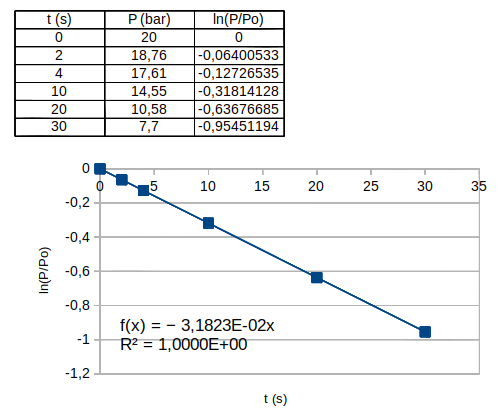
Relis mon message précédent et revois si nécessaire ton cours sur les log et les exponentielles. Le coefficient directeur de la droite est -2k...
J'ai trouvé toutes les formules, est ce que vous pourriez me donner la valeur de k car si ça n'est pas divisé par 2 je bloque totalement ....
Merci pour votre réponse ! 
Puisque tu as démontré précédemment :
La droite obtenue a donc pour coefficient directeur (-2k). Par identification :
Je ne vois pas ce qui te gênes...



