Inscription / Connexion Nouveau Sujet
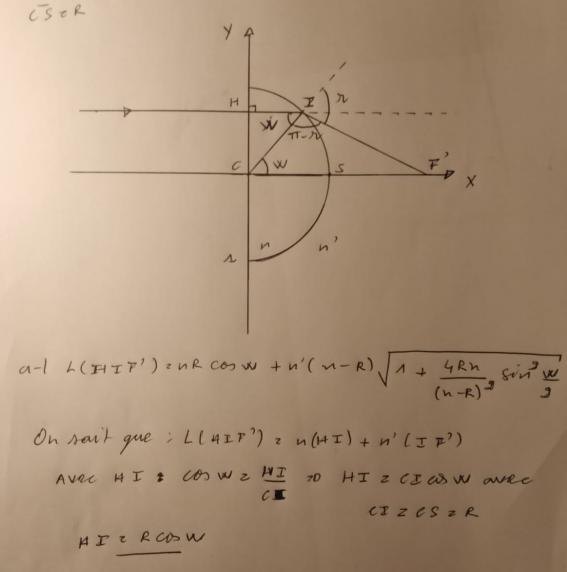
Chemin suivi par la lumiere L(HIF')
Bonjour, je voudrais demontrer que L(HIF')=nRcosw+n'(x-R) avec R=CS et CF'=x.
Je commence ma demonstration on posant L(HIF')= n(HI)+n'(IF')
avec HI=Rcos(w) mais je me bloque quand il s'agit de trouver IF'.
J'aimerais plus d'explication sur la demonstration s'il vous plait.
Bonjour, je voudrais demontrer que L(HIF')=nRcosw+n'(x-R) avec R=CS et CF'=x.
Je commence ma demonstration on posant L(HIF')= n(HI)+n'(IF')
avec HI=Rcos(w) mais je me bloque quand il s'agit de trouver IF'.
J'aimerais plus d'explication sur la demonstration s'il vous plait.
*** message déplacé ***
Bonjour,
Peut-être Pythagore généralisé (Al Kashi ?) dans le triangle CIF' puis un peu de trigo avec
Un peu plus simple dans la mesure où cela fait intervenir indirectement la loi de Descartes sur la réfraction : le théorème des sinus dans un triangle quelconque peut rendre service...
Je viens de terminer le calcul : pas de problème : le résultat s'obtient assez directement avec le théorème d'Al-Kashi ; on peut se passer du théorème du sinus tel que l'exercice est posé.
on se propose d'appliquer le principe de Fermat. Cela revient à chercher pour quelles valeurs de w la dérivée dL/dw est nulle.
*** message déplacé ***
Bonsoir... Pour répondre à la question j'ai fait la dérivée de L (dL) et je trouve une chose qui ne m'avantage pas du tout. J'aimerais avoir votre avis sur la question s'il vous plaît.
** image supprimée => relis l'assouplissement temporaire sur les propositions manuscrites : ![]() [COVID-19] Assouplissements jusqu'à FIN JUIN (présentation comme pour un devoir sur table !) **
[COVID-19] Assouplissements jusqu'à FIN JUIN (présentation comme pour un devoir sur table !) **
*** message déplacé ***
Bonsoir,
Sauf erreur de ma part, il s'agit de la suite du même sujet, donc pas de multi-post :
Concernant les propositions manuscrites, je t'ai mis ci-dessus le lien vers l'assouplissement temporaire en vigueur => pas de brouillon, que des propositions propres (comme pour un devoir sur table)
Bonne soirée
Quelle est la question posée exactement ?
Souvent dans ce genre de problème, on cherche à démontrer que la lentille ne constitue pas un système rigoureusement stigmatique mais qu'il existe un stigmatisme approché dans les conditions de Gauss soit, dans ce contexte, pour des valeurs de  très faibles. Cela permet d'obtenir la valeur de x en fonction de R, n et n'.
très faibles. Cela permet d'obtenir la valeur de x en fonction de R, n et n'.
Je viens de terminer le calcul : pas de problème : le résultat s'obtient assez directement avec le théorème d'Al-Kashi ; on peut se passer du théorème du sinus tel que l'exercice est posé.
Pourrais-tu envoyer la démonstration que tu as réalisé car je suis bloqué avec ce théorème
Pourrais-tu envoyer la démonstration que tu as réalisé car je suis bloqué avec ce théorème
Commence par exposer ce que tu as réussi à faire puis ce qui te bloque.
Comment écris-tu le théorème d'Al-Kahsi ?
Remarque : tu tu ne te sens pas à l'aise avec ce théorème, il te suffit d'écrire la relation vectorielle entre les trois côtés du triangle puis d'élever au carré :
Merci et du coup après on utilise L(HIF')=n(HI)+n'(IF') et je développe mais pour la partie n'(IF') je suis bloqué
Le problème est que je ne sais pas d'où vient la racine c'est sur ça que je suis bloqué car j'obtiens nRcosw + n'(R^2+x^2-2Rx (1-2sin^2(w/2)) et après je ne sais pas
Il suffit de passer à la racine carrée... Si tu as du mal au niveau calcul pour cette question, la suite va te paraître très difficile...


 ) :
) :

