Inscription / Connexion Nouveau Sujet
chauffage gaz parfait
Bonjours j'ai quelque difficulté avec cet exercice. je trouve des résultats un peu curieux pour la première question (par exemple P1= 2...) et je suis incapable de dire qu'elle est la nature de la transformation dans le compartiment 1.
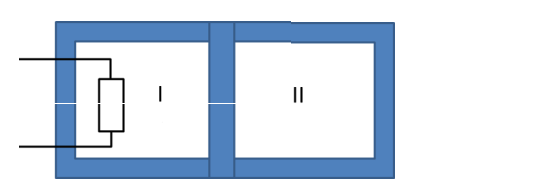
Un cylindre adiabatique est divisé en deux compartiments (I) et (II) par un piston, imperméable à la chaleur, pouvant se déplacer sans frottement. A l'état initial, chaque compartiment contient une mole d'un gaz parfait, sous les mêmes conditions de pression de température (P0 et T0).
Le compartiment (I) contient une résistance électrique de capacité thermique négligeable. On chauffe le gaz du compartiment (I). A l'état final la température du gaz dans le compartiment (II) est égale à T2.
1) Déterminer les conditions finales (P, V et T) sous lesquelles se trouve le gaz dans
chacun des compartiments.
2) Tracer dans le plan (V, P) les deux transformations et indiquer la nature des
transformations.
3) Déterminer pour chaque gaz la variation de l'énergie interne et le travail échangé :
quelle est l'expression de la chaleur fournie par la résistance électrique ?
Bonjour,
Et si tu commençais par proposer des réponses en expliquant éventuellement ce que tu ne comprends pas ? L'aide ultérieure sera plus utile qu'un corrigé "tout cuit" pas nécessairement adapté à ton niveau...
Les deux gaz parfaits ont-ils la même atomicité ? Si oui laquelle ? (à moins que la valeur de  ne soit donnée pour les deux gaz).
ne soit donnée pour les deux gaz).
Quelles sont les données numériques ?
La transformation du gaz n° 1 n'a rien de très particulier : on peut juste affirmer, sans connaître les valeurs numériques : Q1>0 (apport d'énergie thermique grâce à la résistance) ;W1<0 : le gaz 1 fournit du travail au gaz 2 en le comprimant.
Bonjour, 
je ne sais pas plus que ce qui est marqué:  n'est pas donné. les 2 gaz sont identiques. il n'y a pas de valeurs numériques. on doit trouver P1, V1 T1, P2 et V2 à partir de T2. (du moins c'est ce que je comprends. )
n'est pas donné. les 2 gaz sont identiques. il n'y a pas de valeurs numériques. on doit trouver P1, V1 T1, P2 et V2 à partir de T2. (du moins c'est ce que je comprends. )
je les trouve à partir de la loi de Laplace:
V2 =V0 (T0/T2)1/ -1
-1
P2 =P0 (T0/T2)1/1-
V1=2V0 - V1
P1 = P0(V0 /(V1)
T1 =T0(V0 /(V1)
Ensuite je comprends bien que la transformation dans le compartiment II est une transformation adiabatique. Mais pour le compartiment I que faire? la pression change, le volume change Q n'est pas cst. il ne reste pas que la température. je suppose donc que la réponse est isobare mais je ne sais pas vraiment comment le trouver.
Tu as raison en ce qui l'application de la loi de Laplace au gaz n°2. En revanche, le gaz n° 1 ne subit pas une évolution adiabatique réversible : la loi de Laplace ne s'y applique pas.
Quelques indications :
L'état final est un état d'équilibre mécanique du piston mobile : P1=P2
La somme des deux volumes est une constante : V1=2Vo-V2
Ensuite : premier principe appliqué à l'ensemble des deux gaz, sachant que l'énergie interne est une fonction d'état extensive :  U=
U= U1+
U1+ U2=Q1 ; tu couples cette relation avec la première loi de Joule et la suite est facile bien qu'un peu "calculatoire" puisque tout doit être fait littéralement.
U2=Q1 ; tu couples cette relation avec la première loi de Joule et la suite est facile bien qu'un peu "calculatoire" puisque tout doit être fait littéralement.


