Inscription / Connexion Nouveau Sujet
Changement de referentiel
Bonjour, j'aimerais un peu d'aide pour cet exercice. Merci
ENONCE
Les berges d'un fleuve sont parallèles et la distance qui les sépare
est d = 400 m. On suppose que la vitesse de l'eau est constante et
egale à . Un bateau part d'un point A sur une berge et veut atteindre le point B situé sur l'autre rive, exactement en face de A, selon une trajectoire rectiligne.
Pour ce faire, il part de A avec une vitesse relative constante faisant un angle
 avec la berge. Il atteint B au bout d'une durée t.
avec la berge. Il atteint B au bout d'une durée t.
1.Determiner la vitesse relative Vr et l'angle .
Application numérique : u = 2m/s ; l = 400m ; t = 25 min
Le bateau part maintenant d'un point A d'une berge avec une vitesse relative constante pour atteindre un point C quelconque de l'autre berge.
2.Determiner l'orientation de pour que la durée de la traversée soit minimale.
3.Quelle est cette durée minimale, quel est le chemin alors parcouru ?
PISTES DE RECHERCHES
1. Vr = l/t = 0.3 m/s
je n'arrive pas à trouver l'angle
Merci de m'aider
Bonjour
Il faut utiliser la composition des vitesses : en vecteur :
La vitesse absolue (celle du bateau par rapport à la berge) est égale à la somme de la vitesse relative (celle du bateau par rapport à l'eau) et de la vitesse d'entraînement (celle de l'eau par rapport à la berge).
Aide-toi d'un schéma que tu pourras éventuellement scanner et poster ici.
Je te olaisse réfléchir et poster une solution.
Vous ne m'avez pas répondu pour la 1ere question.
J'ai trouvé Vr = 0,3 m/s. et phi =π/2
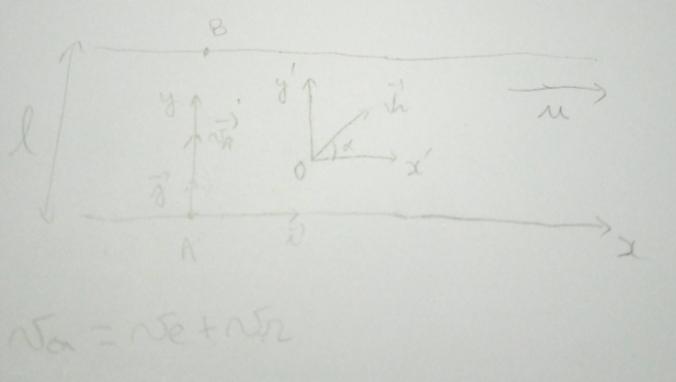
2- On a deux référentiels : un référentiel absolu d'origine A
et un référentiel relatif d'origine l'eau ayant tous deux leurs axes parallèles
Tu n'as pas compris. La vitesse du bateau par rapport à la terre, c'est à dire la vitesse absolue doit être orientée de A vers B, le point sur l'autre berge en face de A. Le point C de ta figure est sans intérêt. Tu connais la vitesse d'entraînement : celle de l'eau par rapport à la terre :
Ces deux vecteurs sont parfaitement définis, à la fois en direction, en sens et en norme puisque :
où l désigne la largeur du fleuve, également notée ”d” dans ton énoncé...
Facile alors d'obtenir le vecteur vitesse relative puisque :
Tu postes au niveau math spé : j'imagine que tirer les conséquences d'une soustraction de deux vecteurs ne te pose pas de difficulté. Tu peux évidemment t'aider d'un schéma où seront représentés les divers vecteurs vitesse.
la chose qui m'a melangé c'est que dans l'énoncé c'est dit :
Pour ce faire, il part de A avec une vitesse relative constante
 avec la berge
avec la bergec'est comme si en A il avait deja la vitesse relative
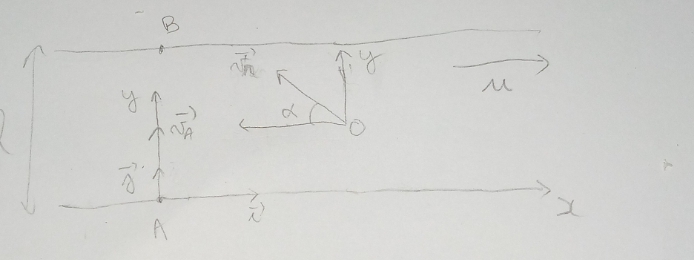
Ta figure ne précise pas le repère de projection et les vecteurs unitaires ; difficile de vérifier tes résultats...
Autre chose : cet énoncé ne semble pas se préoccuper du nombre de chiffres significatifs ; dans ces conditions, pour ne pas risquer d'être pénalisé un jour de concours ou d'examen, il est préférable de conserver en mémoire de la calculatrice tous les chiffres significatifs pour arrondir seulement le résultat final. Trop d'arrondis dans les calculs intermédiaires finissent par fournir au final un résultat erroné. Il ne faut pas arrondir la norme du vecteur vitesse absolue à 0,3m/s pour le calcul de la norme du vecteur vitesse relative.
Représente les trois vecteurs vitesse sur la figure. Tu verras qu'il est assez facile alors d'obtenir la valeur de l'angle  .
.
OK pour le repère et les vecteurs et
mais le représentant du vecteur
?
Ce tracé te permettra de visualiser l'angle  puis de le calculer. Au niveau math spé, cela ne devrait pas poser de problème, surtout après le rappel de krinn dans son récent message du 09-09-21 à 20:27 !
puis de le calculer. Au niveau math spé, cela ne devrait pas poser de problème, surtout après le rappel de krinn dans son récent message du 09-09-21 à 20:27 !
Il te faut reprendre le calcul des normes des différents vecteurs vitesse en tenant compte de mes remarques sur le nombre de chiffres significatifs.
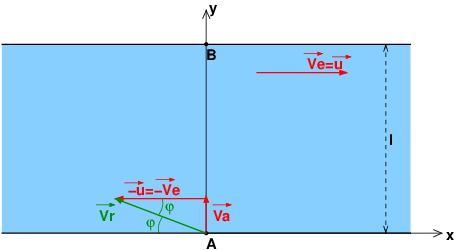
Ta représentation de est totalement irréaliste ! le courant tend à entraîner le bateau dans le sens du courant donc dans le sens positif de l'axe (Ax). Pour que le bateau puisse se déplacer en ligne droite vers B, il faut nécessairement que le vecteur
ait une composante négative suivant l'axe des x .
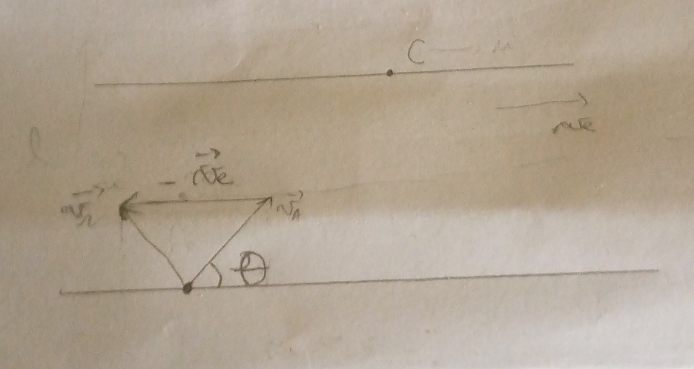
Le schéma ci-dessous devrait t'aider. Attention : il n'est pas à l'échelle pour plus de clarté. Je n'y ai fait qu'illustrer la relation vectorielle :
Reprends aussi le calcul de la norme vr en tenant compte de mes précédentes remarques.
Merci bien
Le bateau part maintenant d'un point A d'une berge avec une vitesse relative constante pour atteindre un point C quelconque de l'autre berge.
Quelle serait la différence entre le premier schéma et celui que je dois représenter pour cette deuxième partie ?
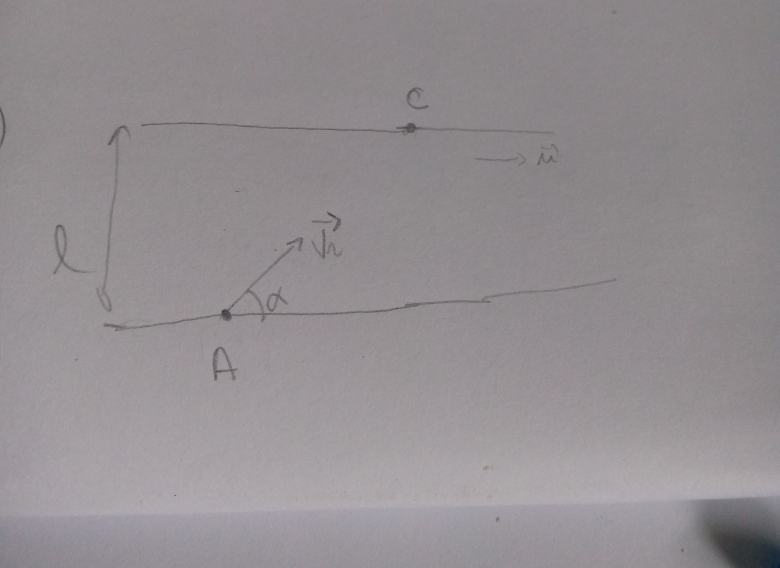
Le vecteur est maintenant orienté de A vers C ; l'angle
 entre l'axe (Ax) et ce vecteur peut prendre une valeur quelconque telle que :
entre l'axe (Ax) et ce vecteur peut prendre une valeur quelconque telle que :
0< <
< (en radians).
(en radians).
mais pourquoi dans les deux questions, les énoncés disent qu'il part du point A avec une vitesse relative ?
Normalemant en A c'est la vitesse absolue.
Je n'arrive pas à comprendre
Puisque est un vecteur constant et que
est aussi un vecteur constant, le vecteur somme, c'est à dire le vecteur
est aussi un vecteur constant au cours du mouvement ; le mouvement de A à C est un mouvement rectiligne uniforme. En tout point de la trajectoire, c'est à dire du segment [AC], les trois vecteurs existent avec la relation entre les trois :
Ton message de 12h48 n'a pas de sens dans ces conditions, même s'il est commode de représenter, comme je l'ai fait, les trois vecteurs vitesse au point A.
Il faut reprendre la représentation des trois vecteurs vitesse sur le modèle de mon schéma mais avec un vecteur maintenant orienté de A vers C , soit incliné de l'angle
 quelconque par rapport à l'axe (Ax).
quelconque par rapport à l'axe (Ax).
Tu n'as sans doute pas le temps d'utiliser un logiciel pour le schéma mais essaie tout de même de faire quelque chose de propre et de soigné : traits tirés à la règle, indication claire des angles...
2.Determiner l'orientation de pour que la durée de la traversée soit minimale.
L'espace laissé en blanc correspond à la vitesse absolue ou à la vitesse relative ? Selon la réponse à cette question, il faudra privilégier dans les calculs l'angle
 ou l'angle
ou l'angle  . ???
. ???2.Determiner l'orientation de \vec{V_r} pour que la durée de la traversée soit minimale.
Voici comment j'ai fait
et donc
Non ! tu raisonnes comme si l'angle  était onfondu avec l'angle
était onfondu avec l'angle  . Ces deux angles ne sont pas égaux a priori !
. Ces deux angles ne sont pas égaux a priori !
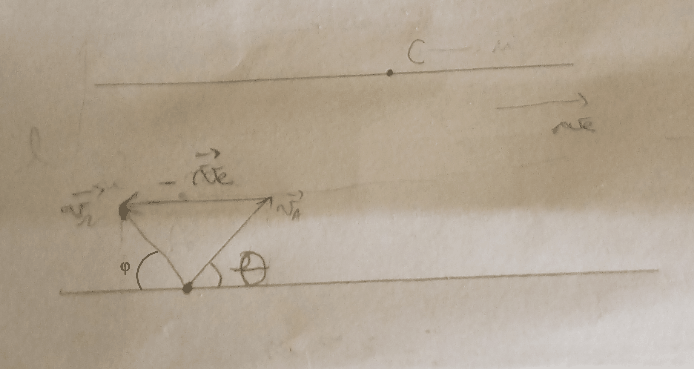
Non ! tu raisonnes comme si l'angle
 était onfondu avec l'angle
était onfondu avec l'angle  . Ces deux angles ne sont pas égaux a priori !
. Ces deux angles ne sont pas égaux a priori !Je n'ai pas bien compris votre remarque
l'angle
 doit il apparaitre dans les coordonnées de Vr ?
doit il apparaitre dans les coordonnées de Vr ?Oui ! C'est d'ailleurs une condition sur
 que l'on obtient de façon très simple pour minimiser le temps de traversée. Je t'ai posé à 15h48 une question pour savoir s'il fallait trouver uniquement la valeur de
que l'on obtient de façon très simple pour minimiser le temps de traversée. Je t'ai posé à 15h48 une question pour savoir s'il fallait trouver uniquement la valeur de  ou également la valeur de
ou également la valeur de  minimisant la durée de traversée. Tu ne m'as pas répondu.
minimisant la durée de traversée. Tu ne m'as pas répondu.OK ; commence effectivement par trouver la condition sur  qui minimise la durée de traversée. Le résultat est très simple mais demande à être démontré rigoureusement...
qui minimise la durée de traversée. Le résultat est très simple mais demande à être démontré rigoureusement...
Comme je l'avais dit :
(1)
Or,
et
en remplaçant dans (1), j'obtiens :
Pour que t soit minimal il faut que sin soit maximale ( sin
soit maximale ( sin =1)
=1)
Ainsi  =
=  /2
/2
C'est bien cela ! 
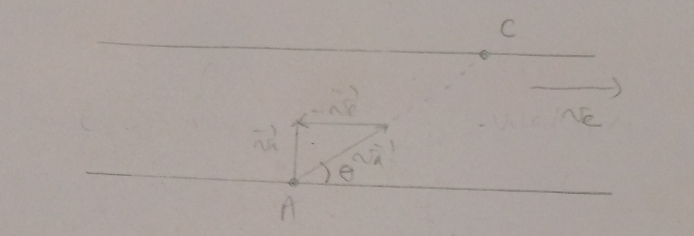
La suite est facile. Là encore, tu as intérêt à faire un schéma représentant les trois vecteurs vitesse dans le cas  =
= /2 rad
/2 rad
Le schéma devient donc :
Pour la durée minimale, je remplace  dans (*) j'obtiens
dans (*) j'obtiens
Ce qui est logique car moins C est éloigné moins sera la durée de traversée
Ce qui est logique car moins C est éloigné moins sera la durée de traversée
Rectificatif : moins C est éloigné de B