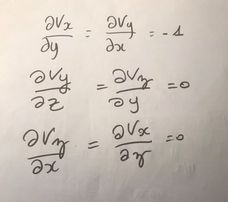Inscription / Connexion Nouveau Sujet
Champs vectoriel et gradient
Bonjour, je n'arrive pas à trouver la fonction scalaire dans cet exercice. J'ai montré que est un gradient et je sais qu'on doit associer l'opérateur gradient à une fonction
scalaire.
Pouvez-vous m'expliquer ?
Ci-dessous la consigne :
On considère le champ vectoriel :
Montrer que ce champ est un gradient (je l'ai fais et c'est juste), et déterminer la fonction scalaire dont il dérive par la relation
Cordialement
OK, donc par
Parce qu'une autre manière est de montrer que existe, ce qui fait qu'on traite les deux questions en une.
Il suffit d'exprimer les trois composantes du gradient et montrer qu'elles sont bien les dérivées d'une même fonction.
Alors j'ai trouvé une correction et je ne comprend pas pourquoi après avoir intégré on rajoute une fonction avec différentes variables pour chaque composante du gradient.
ex : Pourquoi rajouter une fonction qui dépend de ces variables à cette composante du gradient ?
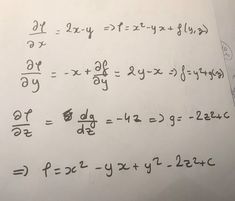
C'est la notion de dérivé partielle qui est en cause : quand vous intégrez , vous trouvez comme pour toute intégration
sauf que, par définition, la dérivation partielle par rapport à x suppose que y et z sont maintenus constants et donc K=K(y,z).
Merci, mais pourquoi quand on intègre on trouve - yx ? Dans ce cas ne devrait on pas également multiplier x^2 par x ?
Je ne comprends pas trop la question :
avec y constant donne bien
La primitive de 2x c'es bien x2, et celle de y (qui est une constante) c'est bien yx
Autant pour moi, c'est pcq y est considéré comme une constante vu que c'est une dérivée partielle par rapport à x et que le primitive d'une constante est kx.