Niveau maths sup

Champs électrostatique

Posté par
qnouro 11-06-16 à 01:47

Bonjour/Bonsoir,
J'ai beaucoup de mal à définir les plans de symétrie /d'anti-symétrie ainsi que les invariances et surtout les charges élémentaires.
c'est encore pire en coordonnées cylindrique ou sphériques :/
Pourriez-vous me donner des "astuces" afin de les repérer ?
Voici deux situations qui serviront d'exemple :
Arc de cercle de rayon R chargé uniformément en longueur (lambda)
Cylindre de rayon R et d'axe (Oz) uniformément chargé en surface (sigma)
Merci d'avance , Cordialement.

Posté par re : Champs électrostatique 11-06-16 à 12:10

Bonjour
J'ai eu l'occasion de créer il y a quelque temps une fiche sur ce sujet. Elle pourra peut-être t'aider. Sinon, les plans de symétrie de la source se définissent comme en math. Cependant, il est très important de remarquer que seuls les plans de symétrie de la source contenant le point M où on cherche à déterminer le vecteur champ présentent de l'intérêt.
Il s'agit de la fiche n° 3 :

Posté par re : Champs électrostatique 11-06-16 à 12:42

Bonjour,
Merci infiniment de m'avoir répondu.
En effet je n'avais pas vu qu'une fiche existait déjà, erreur de ma part.
Cependant, je n'y vois pas comment déterminer les charges élémentaires (et plus précisément les vecteurs élémentaires de déplacement dl,dS ou dV).
Par exemple dans la correction du premier cas que j'ai cité : dq = lambda * R * dtheta mais je ne comprend pas comment aboutir à ce résultat.
Pourriez-vous éclairer ma lanterne d'avantage ?
Cordialement,

Posté par re : Champs électrostatique 12-06-16 à 17:09

Bonjour
Pour aborder la physique au niveau indiqué par ton profil, il y a un minimum d'acquis en mathématique indispensables. Savoir qu'une rotation d'un angle (mesuré en radians) d'un point sur un cercle de rayon R correspond à une distance parcourue égale à R. fait partie de ces acquis indispensables...
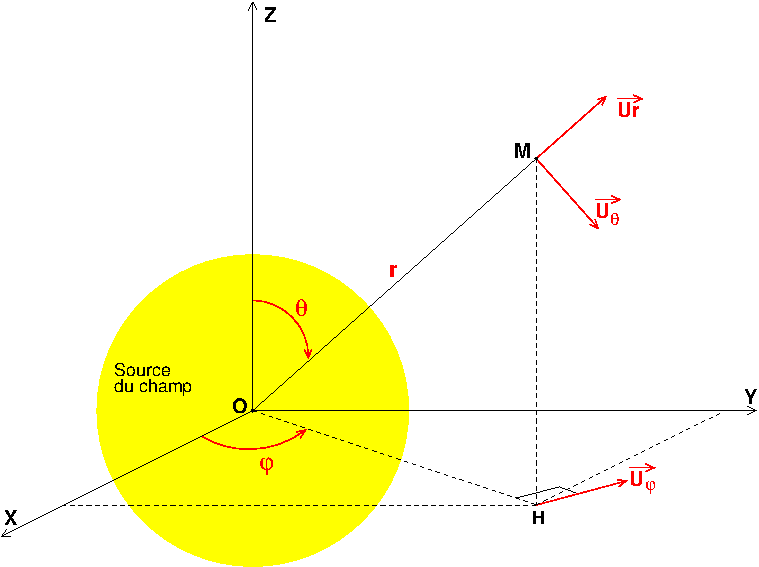
Pour les déplacements élémentaires exprimés en coordonnées sphériques, il faut imaginer successivement trois déplacements élémentaires :
1° variation de r de dr à et fixes : déplacement élémentaire : $\overrightarrow{dl_{1}}=dr\cdot\overrightarrow{u_{r}}$
2° variation élémentaire de à r et fixes : rotation de d sur un cercle de rayon r : $\overrightarrow{dl_{2}}=r\cdot d\theta\cdot\overrightarrow{u_{\theta}}$
3° variation élémentaire de à r et fixes : rotation de d sur un cercle de rayon r.sin() : $\overrightarrow{dl_{3}}=r\cdot\sin\left(\theta\right)\cdot d\varphi\cdot\overrightarrow{u_{\varphi}}$
L'expression la plus générale du déplacement élémentaire est la somme vectorielle des trois précédents :

$\overrightarrow{dl}=dr\cdot\overrightarrow{u_{r}}+r\cdot d\theta\cdot\overrightarrow{u_{\theta}}+r\cdot\sin\left(\theta\right)\cdot d\varphi\cdot\overrightarrow{u_{\varphi}}$

Une surface élémentaire s'obtient en effectuant le produit de deux de ces trois déplacements élémentaires. Par exemple : un petit élément de surface sur une sphère de rayon R aura pour expression (sachant que r = R) :

$dS=r\cdot d\theta\cdot r\cdot\sin\left(\theta\right)\cdot d\varphi$
Tu peux t'entraîner à démontrer à partir de ce résultat que l'aire d'une sphère vaut $4\pi R^{2}$ ...
Un volume élémentaire s'obtient en multipliant les trois déplacement élémentaires :

$d\tau=r\cdot dr\cdot r\cdot d\theta\cdot r\cdot\sin\left(\theta\right)\cdot d\varphi$
Tu peux t'entraîner à démontrer à partir de ce résultat que le volume d'une boule de rayon R vaut : $\frac{4}{3}\pi R^{3}$ ...
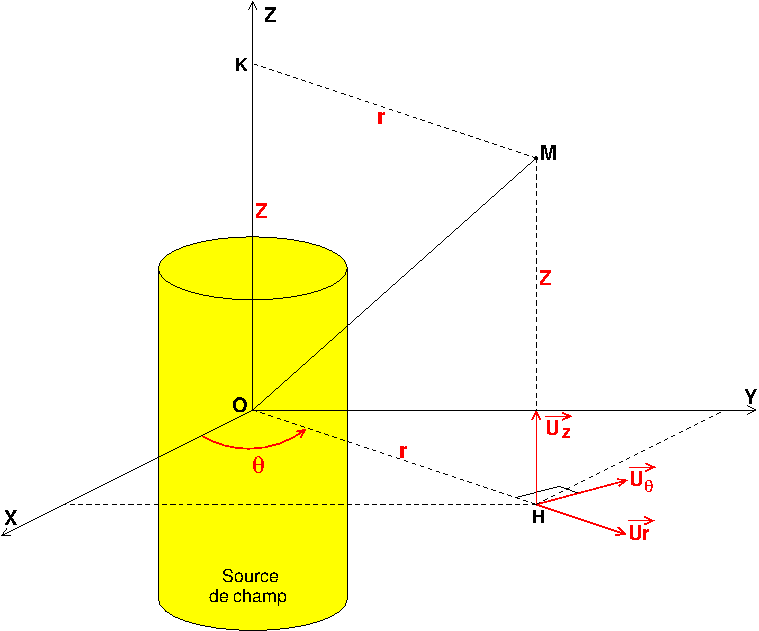
Pour les coordonnées cylindriques, utilise le schéma pour obtenir le résultat suivant :

$\overrightarrow{dl}=dr\cdot\overrightarrow{u_{r}}+r\cdot d\theta\cdot\overrightarrow{u_{\theta}}+dz\cdot\overrightarrow{u_{z}}$

Champs électrostatique