Inscription / Connexion Nouveau Sujet
Champ tournant
Bonjour.
Mon exercice s'intéresse au principe de création d'un champ tournant.
On utilise deux bobines identiques parcourues par des courants sinusoïdaux de même amplitude, de même fréquence avec un déphasage de  /2.
/2.
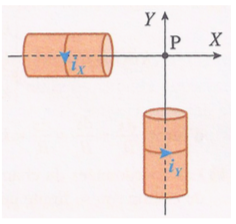
On place les bobines à angle droite (cf. schéma joint) et on note P le point d'intersection entre les deux axes des bobines.
Je dois déterminer le champ magnétique résultant en P.
Première étape, j'ai écrit l'expression vectorielle du champ magnétique créé par une bobine : ou u indice Y (c'est selon),
 est l'angle sous lequel on voit le haut de la spire au point M.
est l'angle sous lequel on voit le haut de la spire au point M.
Et j'ai aussi :
(le signal déphasé)
Mais je ne sais pas comment continuer : je ne peux pas additionner les champs puisque les bobines n'ont pas le même axe.
Quelle est la méthode ?
Merci par avance pour vos réponses 
Bonjour
Tu peux appliquer le théorème de superposition en considérant le vecteur champ comme la somme des deux vecteurs champs créés par les deux bobines. Selon la loi de Biot et Savart, chaque vecteur champ a une valeur algébrique proportionnelle à l'intensité, les deux constantes de proportionnalités étant les mêmes si les bobines sont identiques et placées à la même distance de P. Ainsi le vecteur champ en P peut s'écrire :
Je te laisse continuer... Poste à nouveau si tu ne t'en sors pas...
Remarque : l'expression de B que tu as obtenue correspond au champ créé par une seule spire, tu as ici une bobine longue apparemment... Peut-être que la valeur de K n'est pas demandée et qu'il s'agit juste de démontrer que la norme de B reste fixe et que le vecteur tourne à la vitesse angulaire  dans un sens que je te laisse déterminer...
dans un sens que je te laisse déterminer...
Bonjour vanoise, merci pour ta réponse.
Mon cours ne mentionne pas la loi de Biot de Savart (est-ce au programme, je ne sais pas, mais au vu de ce que tu as répondu je vais l'ajouter quand même). Donc je ne sais pas à quoi correspond ton K.
Mon cours ne mentionne pas la loi de Biot de Savart
Peut-être est-ce parce que nous n'avons pas encore suffisamment avancé dans ce cours.
Tu as raison, la loi de Biot et Savart vient d'être supprimée des programmes de Sup et Spé...
Dans ce cas, fais le raisonnement en gardant la constante K.
Pour info, mais je ne pense pas que cela soit au programme, l'expression de K est :
avec :
N : nombre de spires ; L : longueur de la bobine ;
 1 angle entre entre l'axe et la droite passant par le point P et un point de la spire la plus éloignée ;
1 angle entre entre l'axe et la droite passant par le point P et un point de la spire la plus éloignée ;
 2 angle entre entre l'axe et la droite passant par le point P et un point de la spire la plus proche ;
2 angle entre entre l'axe et la droite passant par le point P et un point de la spire la plus proche ;
Il y a quand même une formule comme ça dans mon cours.
Mais c'est l'expression d'un champ magnétique, avec I, l'intensité du courant en plus.
Mais c'est l'expression d'un champ magnétique, avec I, l'intensité du courant en plus.
As-tu bien compris ce que j'appelle K ici ? Même si la loi de Biot et Savart n'est plus au programme, tu dois savoir que les composantes du champ champ d'induction magnétique créé par un circuit parcouru par un courant sont proportionnelles à l'intensité du courant, la constante de proportionnalité que je note K dépendant de la géométrie du circuit et de la position du point P où on détermine le champ...
L'expression que j'ai donnée dans mon message précédent correspond à une bobine longue, le point P étant sur son axe de symétrie. Pour le champ créé par la bobine n° 1 seule, on obtient au point P :
Ce qui est cohérent avec l'expression de K que j'ai fournie et avec ton formulaire. Si tu n'as pas suffisamment de renseignements sur les bobines, ce n'est pas grave, fais le raisonnement en conservant l'inconnue K : l'essentiel est tout de même de montrer que l'on obtient en P un vecteur résultant
 autour d'un axe (O,Z) perpendiculaire au plan de figure.
autour d'un axe (O,Z) perpendiculaire au plan de figure.
P.S. : es-tu certaine du signe "-" dans l'expression de iY ?
Mais c'est l'expression d'un champ magnétique, avec I, l'intensité du courant en plus.
As-tu bien compris ce que j'appelle K ici ? Même si la loi de Biot et Savart n'est plus au programme, tu dois savoir que les composantes du champ champ d'induction magnétique créé par un circuit parcouru par un courant sont proportionnelles à l'intensité du courant, la constante de proportionnalité que je note K dépendant de la géométrie du circuit et de la position du point P où on détermine le champ...
Je me suis mal exprimée dans mon message précédent : oui, on a effectivement dans le cas général
Deuxième point, pour le "-" j'ai fait une erreur avec iY(t).
Rectification :


 est l'angle polaire entre les vecteurs
est l'angle polaire entre les vecteurs 
