Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

Champ magnétostatique

Posté par
GFC03 21-03-23 à 18:18

Bonsoir j'ai un exercice dans le quel on me demande de trouver le champ magnétique en un point de l'axe d'un demi-cylindre de longueur infini parcourus par un courant uniforme

Posté par
GFC03re : Champ magnétostatique 21-03-23 à 18:32

Correction :
Il y a invariance par translation et par rotation par rapport à z le plan formé par\vec{u_\theta }  et  \vec{u_r} est un plan d'anti symétrie pour la distribution donc\vec{ B} appartient à ce plan.
Mais à partir de là je suis bloqué

Posté par
vanoisere : Champ magnétostatique 21-03-23 à 18:35

Bonjour
Une méthode assez simple possible consiste à découper le demi cylindre en fils élémentaires parallèles à l'axe (Oz) , d'axes repérés par les coordonnées cylindriques (r,)de sections droites élémentaires d'aire dS=r.dr.d.
Tu exprimes le vecteur champ élémentaire créé par ce cylindre élémentaire puis tu intègres.
Attention : comme d'habitude dans ce genre de problème, étudier les symétries et les invariances de la source de champ.
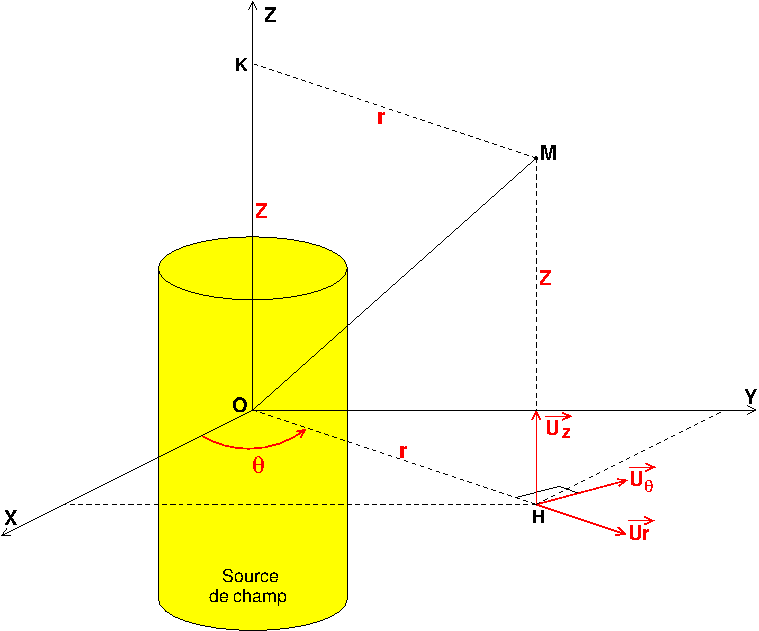
Ci-dessous : figure rappelant les coordonnées cylindriques (ou cylindro-polaires). Adapter la figure au problème bien sûr.

Champ magnétostatique

Posté par
GFC03re : Champ magnétostatique 22-03-23 à 10:07

Bonjour
Le champ élémentaire créé par un fil élémentaire à la distance r de l'axe (oz) est est porté par \vec{u_\theta } ,
Et s'exprime dB=\frac{ \mu_0dI}{2\pi r}=\frac{\mu_0jds }{2\pi r} avec ds=rdr.d\theta on aura
B=\int\int \frac{\mu_0 drd \theta }{2\pi }\Rightarrow \vec{B}=\frac{\mu_0 r }{2}\vec{u_\theta }
Est ce correct?

Posté par
vanoisere : Champ magnétostatique 22-03-23 à 10:54

Ton expression de d\vec B est correcte mais pas celle de \vec B. Qu'as-tu fait de j ? j s'exprime simplement en fonction de l'intensité I et de R, le rayon du demi cylindre.
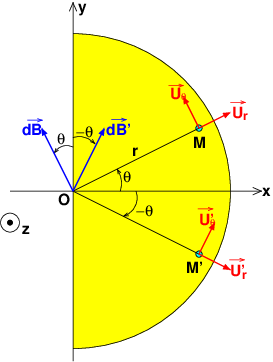
Avant t'intégrer, raisonne sur les symétries du demi cylindre pour obtenir la direction de \vec B. Tu verras que ce ne sont pas les normes des vecteurs champ élémentaire qu'il faut additionner mais seulement une de leurs composantes. Pour bien comprendre, tu as intérêt à faire un schéma soigné avec le plan (Oxy) comme plan de figure.

Posté par
GFC03re : Champ magnétostatique 22-03-23 à 20:34

Bonsoir désolé j'ai oublié de mettre le j dans l'expression . En utilisant le schéma que vous avez donné plus haut le champ créé par le demi cylindre obtenu en découpant le cylindre en deux par rapport au plan (oxz) est porté par (ox) .
Mon raisonnement est il correct ?

Posté par
vanoisere : Champ magnétostatique 22-03-23 à 22:00

On peut trouver un plan de symétrie à la source de champ contenant l'axe (Oz). Supposons qu'il s'agisse du plan (Oxz). Que peut on dire de la direction du vecteur B dans ces conditions ? Influence de cette remarque sur le calcul de B ?

Posté par
GFC03re : Champ magnétostatique 22-03-23 à 22:58

Dans ce cas B est perpendiculaire au plan (oxz) et est donc porté par (oy) le champ cherché s'obtient donc en intégrant la composante suivant oy du champ élémentaire obtenu précédemment ce qui donne \vec{B}=\int \int \frac{\mu_0jdrd\theta sin\theta}{2\pi}\vec{j}\Rightarrow \vec{B}=-\frac{\mu_0jr}{\pi}\vec{j} est ce correct ?

Posté par
vanoisere : Champ magnétostatique 23-03-23 à 12:29

Observe bien la figure fournie ci-dessous. Je pense que les notations sont explicites.

Champ magnétostatique

Posté par
GFC03re : Champ magnétostatique 23-03-23 à 14:24

Merci . Dans ce cas là somme des contributions de M et M' donnent dB\vec{u_y}=2dBcos\theta\vec{u_y} en faisant varier \theta
de 0 à π/2 j'obtiens  \vec{B}= \frac{\mu_0jr}{\pi}\vec{j} ce que je ne comprends pas car en prenant seulement M j'obtiens B=0

Posté par
vanoisere : Champ magnétostatique 23-03-23 à 14:55

De bonnes choses et quelques étourderies dans ce que tu écris. Je reprends le calcul sachant que la composante sur y du vecteur champ élémentaire créé au point O par le fil centré en M est :

dB_{y}=\frac{\mu_{o}.j}{2\pi}\cdot dr.\cos\left(\theta\right).d\theta

Intégration sur le demi cylindre :

B_{y}=\frac{\mu_{o}.j}{2\pi}\cdot\int_{0}^{R}dr.\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos\left(\theta\right).d\theta=\frac{\mu_{o}.j.R}{2\pi}\cdot\left[\sin\left(\theta\right)\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}

La fonction sinus étant impaire, cela est équivalent à :

B_{y}=\frac{2\mu_{o}.j.R}{2\pi}\cdot\left[\sin\left(\theta\right)\right]_{0}^{\frac{\pi}{2}}

Reste pour finir à exprimer j en fonction de I et de R.

Posté par
GFC03re : Champ magnétostatique 23-03-23 à 15:37

D'accord pour un demi cylindre j= 2I/(πR²)
Donc \vec{B}=\frac{2\mu_0I}{\pi²R}\vec{j}

Posté par
vanoisere : Champ magnétostatique 23-03-23 à 15:54

D'accord !

Posté par
GFC03re : Champ magnétostatique 23-03-23 à 16:04

Merci beaucoup Vanoise


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !