Inscription / Connexion Nouveau Sujet
Champ Électrostatique
Bonsoir,
Merci. 
On considère un champ électrostatique créé dans un vide par une distribution de charges à symétrie sphérique. La composante radiale de ce champ dépend de la distance au centre
de la distribution selon :
Dans ce problème, la densité volumique de charges vérifie :
1) Donner les différentes variables dont dépend le champ électrostatique en coordonnées sphériques ?
Quelle est la direction direction du champ électrostatique ?
2) On suppose qu'il n'y a pas de charges à l'infini et que les charges infiniment éloignées n'interagissent pas entre elles.
Trouver l'expression du potentiel .
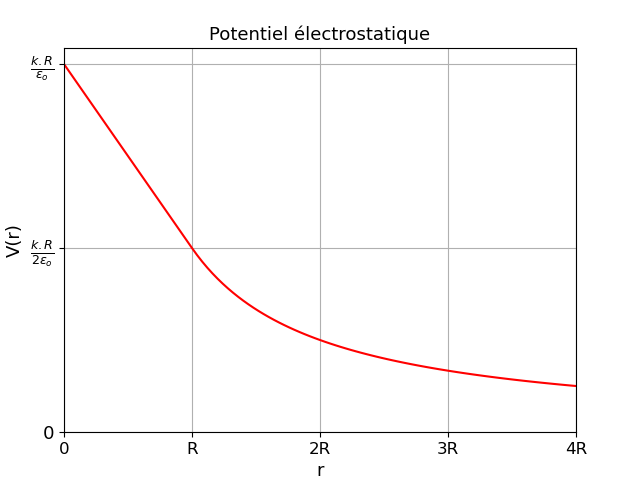
3) Tracer l'allure de en fonction de
.
4) Trouver l'expression de la densité volumique de charges
5) Tracer l'allure de la densité volumique de charges en fonction de .
6) Trouver l'expression de la charge d'une couche sphérique de centre
comprise entre
et
7) Déduire alors l'expression de la charge totale de la distribution en fonction de
et
8) Etablir que pour , on a l'équivalence de cette distribution avec une charge électrique ponctuelle dont on donnera la valeur et la position.
9) On considère maintenant deux charges ponctuelles et
placées à une distance
l'une de l'autre en
et
respectivement. On notera
.
10) Donner l'expression de la force exercée par la charge
sur la charge
11) On considère, cette fois ci le point équidistant de
et
. Déterminer la direction du champ électrostatique créé en
par les charges
et
.
12) Donner le sens de ce champ à l'aide d'un schéma.
13) Si calculer la valeur de la norme du champ.
14) Calculer le potentiel créé en
par les charges
et
dans les mêmes conditions qu'à la question 13).
Réponses
1) On a :
en coordonnées cartésiennes.
J'ai du mal à passer en coordonnées sphériques..
Bonjour
Comme toujours en électrostatique, il faut commencer par raisonner sur les symétries et les invariances de la source du champ. Cela permet de répondre de façon précise à la première question. Pour la deuxième, tu connais la relation entre vecteur champ et potentiel.
Je te laisse réfléchir et proposer une solution...
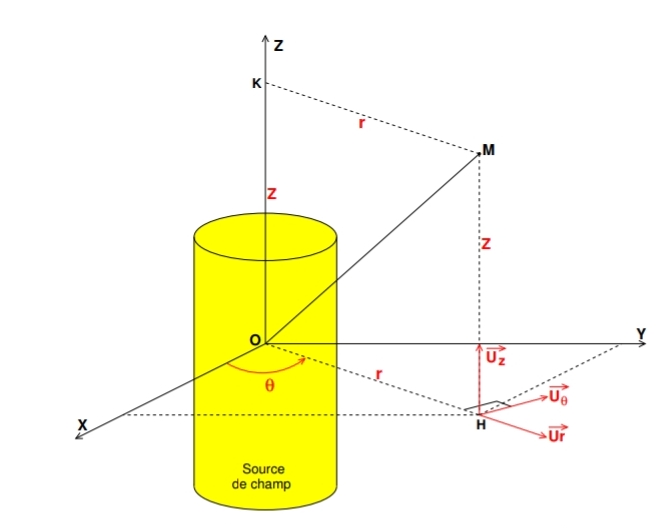
Peut être que l'énoncé devrait nous donner un schéma..
Là j'ai essayé avec le schéma qui se trouve dans mon cours.
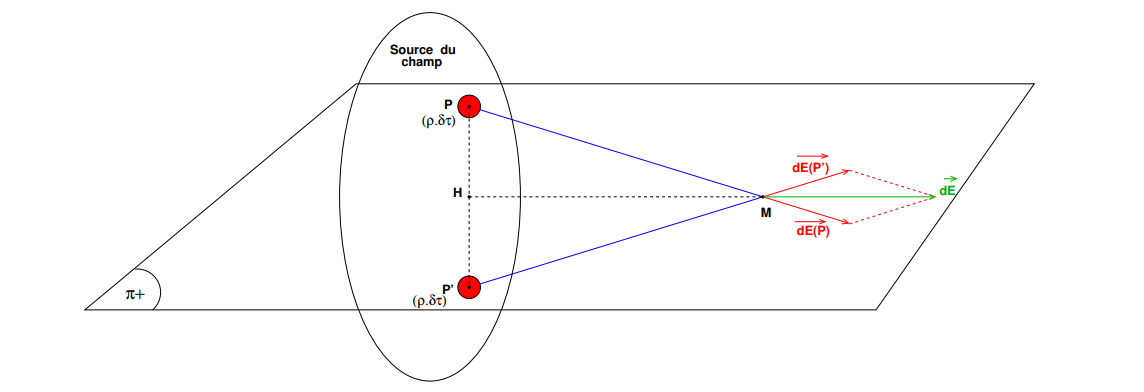
est un plan de symétrie de la source si, à tout point
de la distribution de charge électrique où la densité volumique de charge est
, on peut faire correspondre un symétrique
par rapport à
où la densité de charge est :
D'après l'énoncé, la densité volumique de charges vérifie :
.
Donc
Considérons un volume élémentaire entourant
ou
.
La charge centrée en
crée en
un champ de vecteur :
avec
La charge centrée en
crée en
un champ de vecteur :
P et P' sont symétriques par rapport à : les distances
et
sont égales. La somme des deux vecteurs champ élémentaires s'écrit :
car
(raison de symétrie).
Au final :
Si r > R
La composante radiale du champ électrostatique est proportionnelle à 1/r² pour les distances r supérieures à R. Cela signifie que le champ électrostatique diminue plus rapidement à mesure que la distance augmente.
Là j'ai essayé avec le schéma qui se trouve dans mon cours.
Bizarre... Ce schéma ainsi que l'extrait de démonstration qui l'accompagne sont tirés d'un document que j'ai eu l'occasion d'écrire il y a quelques années et qui est disponible ici :
Le résultat, considéré par la plupart des professeurs comme un résultat de cours, n'a pas nécessairement à être démontré dans un problème mais doit être parfaitement connu : il est énoncé dans la conclusion du paragraphe I du document :
Conclusion : si la source présente un plan de symétrie passant par un point M, le vecteur champ électrostatique ou le vecteur champ de gravitation en M appartient à ce plan de symétrie.
Ici, Tout plan contenant le centre O et un point M de l'espace est plan de symétrie. Pour appartenir à la fois à l'ensemble de ces plans de symétrie, le vecteur champ en M doit être radial.
Il te faut aussi raisonner sur les invariances. La situation de ce problème est étudié au paragraphe VII.1 du même document.
Il y a invariance par rotation d'angle ou
le champ ne dépend que de
, donc
.
Tout point M appartient à deux plans de symétrie et
donc
appartient à leur intersection.
Il est donc porté par .
Le champ est radial :
Le champ électrostatique dépend donc du vecteur en coordonnées sphériques.
La source du champ est invariante par rotation autour du point O : O est centre de symétrie pour la distribution de charge. Les coordonnées adaptées à l'étude sont donc les coordonnées sphériques comme indiqué dans le paragraphe VII.1 du document. Je croyais que tu avais compris puisque, dans ton message du 23-01-23 à 05:13, tu évoquais les vecteurs unitaires et
. Les coordonnées cylindro-polaires sont adaptées aux distributions de charges présentant seulement un axe de symétrie, l'axe (O,z).
Dans ton message du 23-01-23 à 05:13, tu as correctement répondu à la question 1. Tu peux passer à la question 2. Tu as sûrement étudié en cours la relation entre vecteur champ et potentiel.... La situation est très simple ici puisque la distribution de charges est à symétrie sphérique.
Ah désolé, j'ai mal lu ta réponse.
Mais j'aimerais avoir un schéma clair pour la première question.
La relation entre le vecteur champ et le potentiel est définie par la loi de Gauss. Cette loi stipule que le produit scalaire entre le vecteur champ et le gradient du potentiel est égal à la divergence du vecteur champ. Autrement dit, le produit scalaire entre le vecteur champ et le gradient du potentiel est égal à la divergence du vecteur champ. En d'autres termes, le vecteur champ est la dérivée du potentiel.
Attention au signe !
La relation entre vecteur champ et potentiel fournit le potentiel à une constante près.
Pour r supérieur à R ,il suffit de savoir que,en absence de charge à l'infini, V tend vers zéro quand r tend vers l'infini.
Pour r inférieur à R, la continuité du potentiel en r=R permet d'obtenir la constante.
Non. Tu n'as pas corrigé le problème de signe et pas bien compris comment déterminer les constantes que je note K1 et K2. Je corrige :
donc :
*si :
*si r>R :
Pas de charges à l'infini, donc :
Donc : K2=0 . Ensuite : continuité de V(r) en r=R :
; donc :
Ce qui permet d'obtenir K1... Je te laisse calculer K1 et continuer.
En abscisse, tu choisis arbitrairement une échelle correspondant à la valeur R ; en ordonnée, tu choisis arbitrairement une échelle pour la valeur . Ensuite tu places les points de la courbe d'abscisses r=0 et r=R puis tu termines par un tracé à main levée. On te demande l'allure de la courbe, pas un tracé précis.
Voici la courbe V=f(r). Bien sûr il y a continuité du potentiel en r=R mais il y a aussi continuité de la dérivée en r=R d'où l'absence de rupture de pente de la courbe en r=R. Cela s'explique par la continuité de E(r) en r=R. Cela ne serait pas le cas pour une distribution surfacique de charge plutôt que volumique.