Niveau autre

Champ crée par un arc de cercle uniformement chargé

Posté par
fidele11 12-01-22 à 11:59

Bonjour,
J'ai besoin de votre aide pour traiter un exercice d'électrostatique (d'un ancien sujet) sur la détermination du champ électrique crée par un arc de cercle uniformement chargé.

Merci d'avance.

Énoncé:
Partie C : champ d'un demi
-cercle et d'un demi-disque chargés

Un arc de cercle
𝐶𝐶'
, de centre
𝑂 et de rayon 𝑅, d'angle au sommet
2𝛼
, situé dans le plan
𝑥𝑂𝑦,porte une
charge
𝜆 par unité de longueur, repartie uniformément. Soit
𝑂𝑥
la bissectrice de
l'angle 𝐶𝑂𝐶'̂ et
𝑂𝑍 l'axe
perpendiculaire au plan
𝐶𝑂𝐶′. On posera 𝑢 = 𝑧⁄𝑅
.
Q-8) Les composantes du champ électrique en un point 𝑀 de l'axe 𝑂𝑍, de côte 𝑧=OM est :

[la suite de l'énoncé est jointe en image]

Mon début:
Q-8) Pour cette question, je dois déterminer les composantes du champ électrique suivant les axes (Oz) et (Ox).
Pour cela, je considère un élément de longueur de l'arc d'angle au sommet r contenant un point P qui crée un élement de champ dE en M dont , la composante suivant (oz) est dEz=dE.cos∅ et la composante suivant (ox) est dEx=-dE.sin∅
avec ∅ l'angle entre dE et l'horizontale et dE=k.dq/PM².
Après intégration je trouve finalement un résultat étrange de ceux qui sont proposés:

$Ez=\frac{\lambda .z\alpha }{2\pi \epsilon _{0}R^{2}(1+u^2)^(3/2)}$ et
$Ex=-\frac{\lambda .\alpha}{2\pi \epsilon _{0}R(1+u^2)^{3/2}}$

Champ crée par un arc de cercle uniformement chargé

Posté par re : Champ crée par un arc de cercle uniformement chargé 12-01-22 à 12:24

Bonjour
Pour être sûr de ne pas faire d'erreur dans tes projections, il est plus simple d'écrire le vecteur champ élémentaire $\overrightarrow{dE}$ créé en M par la charge élémentaire dq centrée en P, sous la forme :

$\overrightarrow{dE}=\frac{dq}{4\pi.\varepsilon_{o}}\cdot\frac{\overrightarrow{PM}}{\Vert\overrightarrow{PM}\Vert^{3}}$

Aucun schéma n'est fourni ?

Posté par re : Champ crée par un arc de cercle uniformement chargé 12-01-22 à 13:25

Non aucun schéma n'est fourni
(Voir sujet complet joint).
J'ai utilisé le schéma suivant:

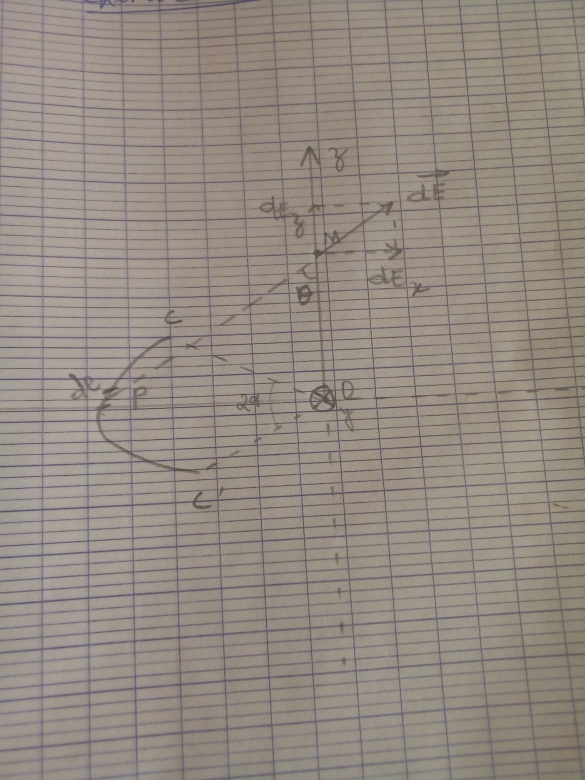
Champ crée par un arc de cercle uniformement chargé

pdf
PDF - 393 Ko

Posté par re : Champ crée par un arc de cercle uniformement chargé 12-01-22 à 14:09

D'accord avec ton schéma. Puisqu'il s'agit d'un QCM, l'objectif est de répondre le plus vite possible en éliminant d'entrée les solution manifestement fausse. En remarquant que le plan (Oxz) contient le point M et est plan de symétrie pour la source de champ : Ey=0. D'après ton schéma et le sens du vecteur champ, on voit que nécessairement :
Ex du signe de - ;
Ez du signe de .
Cela élimine la proposition C. Ensuite, on utilise la méthode que j'ai proposée dans mon message précédent :

$\overrightarrow{PM}=-R.\cos\left(\theta\right).\overrightarrow{i}-R.\sin\left(\theta\right).\overrightarrow{j}+R.u.\overrightarrow{k}\quad;\quad\Vert\overrightarrow{PM}\Vert=R.\sqrt{1+u^{2}}$

$dE_{x}=\dfrac{\lambda.R.d\theta}{4\pi.\varepsilon_{o}}\cdot\dfrac{-R.\cos\left(\theta\right)}{R^{3}.\left(1+u^{2}\right)^{\frac{3}{2}}}$

L'intégration par rapport à va conduire à Ex proportionnel à -.sin(). Inutile d'aller plus loin : la proposition correcte est la B. A titre d'approfondissement, tu peux évidemment terminer le calcul si tu n'es pas en situation de concours ou d'examen.

Posté par re : Champ crée par un arc de cercle uniformement chargé 12-01-22 à 18:03

D'accord, merci bien , je retrouve bien les résultats de la proposition B.
Pour les composantes du champ en O, je trouve seulement suivant l'axe x'x (puisque z=0 de plus) : Ex=λ/(2πε.R) qui serait la proposition C.

Cependant, je peine à trouver le potentiel électrique dans le cas d'un demi-cercle. En effet, j'ai trouvé que le champ électrique pour ce cas de figure (alpha=π/2) est
$E=\frac{\lambda }{2\pi \epsilon _{0}R}[\frac{\sqrt{1+(\pi u/2)^{2}}}{(1+u^{2})^{3/2}}]$ .

Bien qu'on a en vecteur: E=-grad(V) , je n'arrive pas à trouver une primitive de E en fonction de la variable u.

Posté par re : Champ crée par un arc de cercle uniformement chargé 12-01-22 à 18:56

Ce que tu as trouvé concernant la norme E(u) du vecteur champ permet d'éliminer la proposition B. La relation $\overrightarrow{E}=-\overrightarrow{grad}\left(V\right)$ en projection sur l'axe (Oz) conduit à :

$E_{z}=-\frac{\partial V}{\partial z}=-\frac{1}{R}\cdot\frac{\partial V}{\partial u}$

Plutôt que de calculer une intégrale pas très simple, tu testes la relation précédente sur une des deux expressions restantes de V : la A ou la C (a priori la plus simple mais elles sont ici aussi simples l'une que l'autre).

Posté par re : Champ crée par un arc de cercle uniformement chargé 13-01-22 à 09:17

super.
Merci à vous.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Champ crée par un arc de cercle uniformement chargé

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique