Bonsoir
Tu commences par considérer la différentielle de Q  . Or Q n'est pas une fonction d'état. Lors d'un changement d'état ' T est fixe à P fixe.

Merci pour ta réponse, mais je ne saisis pas bien pourquoi l'écriture de la différentielle dH n'est pas acceptable dans le sens où cp et h sont par définition des différentielles partielles et que cette expression fonctionne, par exemple pour les gp :
pour un gp nh = -V d'où dH=cp dT ou bien encore dans le même ordre d'idée,
pour un gp nl=P d'où dU=cv dT

As-tu étudié en cours le diagramme d'équilibre (P,T) d'un corps pur ? On y montre que, pour un équilibre d'un corps pur entre deux phases,  P et T ne sont pas deux variables indépendantes : P=f(T) : équation de la courbe d'équilibre. Or les différentielles que tu as écrites sont valables pour un système fermé en absence de changement d'état, lorsque P et T peuvent varier de façon indépendantes.
Imagine un équilibre liquide vapeur sous la pression P fixe, T est alors obligatoirement fixe. On définit alors l'enthalpie massique de vaporisation Lv=h"-h' où h" est l'enthalpie massique de la vapeur saturante, c'est à dire en équilibre avec du liquide, et où h' désigne l'enthalpie massique du liquide saturant. Lv est une grandeur qui, pour un corps pur donné, dépend de la température. Cette grandeur est aussi parfois appelée "chaleur latente massique de vaporisation". Soit dm la variation de masse de la phase vapeur entre les instants de dates t et (t+dt). La variation élémentaire de masse de la phase liquide entre les mêmes instants est bien sûr (-dm). La variation élémentaire d'enthalpie du système, égale à la quantité élémentaire de chaleur reçue par le système s'écrit :
dH=Q=Lv.dm .
Plus de détail ici :
Pour une étude théorique de la modélisation de la courbe d'équilibre P = f(T) :

N'hésite pas à poser des questions complémentaires si tu le juges utile.

Merci pour ces détails
j'entrevois mon erreur, mais pas encore de manière claire. Je vais donc revoir les notions de différentiation mathématiques, puis reprendrai cette partie du cours de thermodynamique avec une meilleure maîtrise  de la différentiation. Je me laisse le temps de faire cela durant la semaine. Je ne ferme donc pas ce post, et je vous tiens au courant soit pour clore le sujet soir pour quelques questions. En tous cas merci beaucoup pour votre aide

Plusieurs nouvelles questions m'interrogent :
Est ce que toutes les variations des fonctions d'état sont des différentielles exactes ? Si oui pourquoi ? Quelle est la différence entre différentielle totale ou exacte ?
Suite à vos remarques j'ai repris l'étude en différenciant phase monophasique où la variance est de 2 et donc U(T,V) par exemple et la phase diphasique où la variance est de 1, et H=H(P(T)). Pour la première, en suivant vos conseils et quelques lectures j'arrive à trouver l'expression de Q (cf tableau). Cependant dans ces expressions le L et le H ne représentent-ils pas les chaleurs latente à volume et pression constante?,.Pour la phase diphasique où le changement de phase se fait à t et p cte je n'arrive pas à démontrer dH=δQ=chaleur latente.

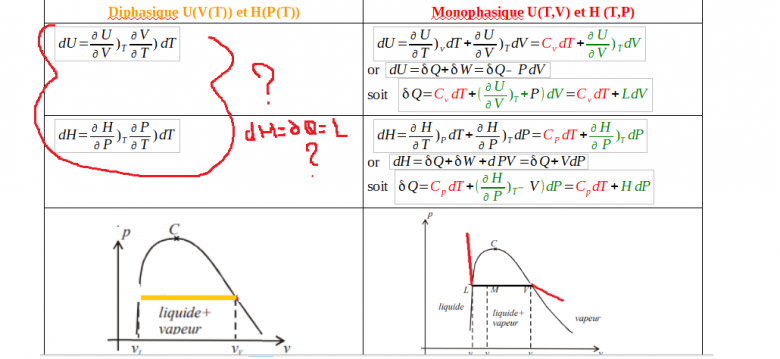
Les variations de fonctions d'état sont toutes des différentielles exactes qui vérifient donc le théorème de Schwarz. En effet, dans un espace à deux dimensions, l'intégration d'une telle différentielle entre deux points ne dépend pas du chemin suivi pour aller d'un point à un autre ; Je te laisse faire la corrélation avec la notion de fonction d'état.

Le tableau que tu présentes ensuite me semble contenir des confusions. Soit un système fermé monophasé régi par une équation d'état f(T,P,V)=0 ; deux variables seulement sont indépendantes lors d'une évolution réversible. On peut écrire indifféremment :

où l est un coefficient calorimétrique homogène à une pression ;

où h est un coefficient calorimétrique homogène à un volume. En appliquant le théorème de Schwarz aux différentielles dU, dS et dH, on démontre :



Cela permet d'obtenir les coefficients l et h si l'équation d'état est connue. Attention : l n'a rien à voir avec une chaleur latente et h n'a rien à voir avec une enthalpie massique !

Tu utilises ensuite un diagramme de Clapeyron pour un corps pur en y traçant une isotherme. L'isotherme est horizontale sous la courbe de saturation : en cas d'équilibre entre deux phases une isotherme est aussi une isobare. Cela se justifie à l'aide de la règle de Gibbs sur la variance d'un système à l'équilibre.

: cela est valide pour toute évolution isobare ou monobare d'un système fermé ; voir éventuellement la démonstration paragraphe 4, ici : Premier principe de la thermodynamique

Une telle variation ou quantité élémentaire ne peut en aucun cas être égale à une chaleur latente massique qui est une quantité finie obtenue expérimentalement. La relation déjà fournie : avec L_v=h'' - h' ne se démontre pas, c'est une relation expérimentale : la variation d'enthalpie lors d'un changement d'état isobare isotherme est proportionnelle à la masse de corps pur qui change d'état.

Bonjour,

Juste une remarque : le problème vient peut-être aussi du fait que dans le cas d'un système diphasique, H est une fonction de trois variables (T,P,x) et donc chercher la différentielle de H en ne faisant intervenir que deux variables T et P  ne peut aboutir.

Le fait de se placer à l'équilibre P(T) ne change pas le problème.

Bonjour
On peut, sous la courbe de saturation introduire la faction massique en vapeur : x mais cela ne change pas le résultat : en se déplaçant sur le palier, on a bien : dH=Lv.dm avec :
dm déjà défini avec précision dans mon message du 17-01-21 à 11:15.
Poser dm=m_t.dx avec : x= m/mt et mt : masse totale du système : (masse liquide + masse vapeur) ne simplifie pas le problème.
L'essentiel à retenir à ce niveau a déjà été écrit je pense... Mais que cela n'empêche pas dim14 de poser des questions supplémentaires s'il le juge utile.

Puisque dim14 s'intéresse aussi aux variations d'énergie interne.
Pour le liquide saturant seul (extrémité gauche du palier) :
h'=u'+P_s.v'
P_s : pression d'équilibre à T donnée : pression de vapeur saturante ;
u' énergie interne massique du liquide saturant seul
v' : volume massique du liquide saturant seul (abscisse de l'extrémité gauche du palier).
Pour la vapeur saturante seule (extrémité droite du palier) on obtient de façon analogue :
h"=u"+P_s.v"
La variation d'énergie interne à P et T fixes s'écrit :
dU=(u"-u').dm=[L_v-P_s.(v"-v')]dm

Merci pour toutes vos réponse, j'y vois plus clair
Maintenant je vais prendre le temps de revoir l'ensemble des td
encore merci à toutes et tous