Inscription / Connexion Nouveau Sujet
centre de gravité et moment d'inertie
Bonjour,
Pour une colle de physique sur la mécanique du solide on nous donne le sujet suivant:
Le référentiel R0 est considéré comme galiléen; il est rapporté au repère(0, x,
x, y,
y, z).
z).
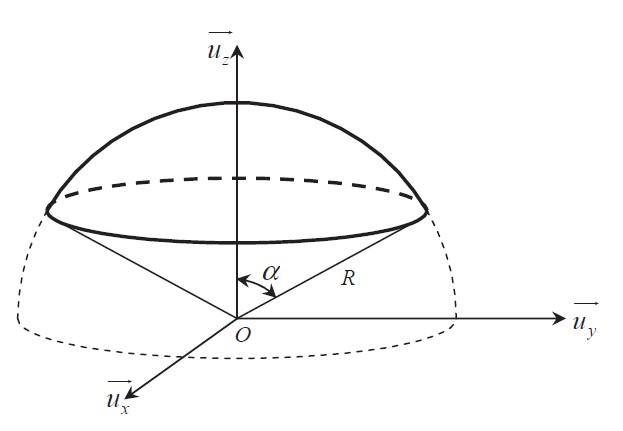
On considère un objet de masse volumique constante ρ ayant la forme d'une portion de sphère pleine de rayon
R, dont le demi angle d'ouverture vaut π/3 (voir schéma ci-dessous).
1.Déterminer la masse M de cet objet en fonction de  et R.
et R.
2. Déterminez la position du centre de masse G de cet objet en fonction de R.
3. Calculez le moment d'inertie de l'objet J(Oz) autour de son axe de révolution Δ(Oz)en fonction de ρ et R, puis en fonction de M et R .
Indication : l'intégrale  3sin 3d
3sin 3d  peut être calculée soit par parties, soit en remarquant que
peut être calculée soit par parties, soit en remarquant que
sin3  =sin
=sin sin²
sin² = sin
= sin (1-cos²
(1-cos² ) .
) .
J'ai répondu à toutes les questions sans pour autant être sur des résultats et j'aimerais connaître la méthode pour déterminer V et S en intégrant car je n'arrive pas à voir d'où vient le sin3 .
.
1.M= V=
V= (Vcône+Vcalotte)
(Vcône+Vcalotte)
M=
2.On a deux plans de symétrie (xOz) et (yOz) donc j'ai est selon l'axe Oz.On applique le théorème de Guldin:
ZG= (S=
)
ZG=
3.J(Oz)=

 (x²+y²)d3m=
(x²+y²)d3m==
Merci d'avance à celui ou celle qui pourras me répondre 
Bonjour
As-tu essayé le "découpage" du solide en tranches parallèles au plan (Oxy) de cotes z et d'épaisseurs dz ? En plus, cela te facilite ensuite le calcul du moment d'inertie car tu connais l'expression de celui d'un disque homogène par rapport à son axe de symétrie.
tu poses : z = R.cos( ) soit dz= -R.sin(
) soit dz= -R.sin( )d
)d avec
avec  compris entre 0 et
compris entre 0 et  .
.
Bonjour,
Non je n'y avait du tout pensé, je vais refaire mes calculs avec cette formule car je pense que mon moment d'inertie est faux du coup, merci 
Une façon parmi d'autres :
Volume de révolution (pour la calotte sphérique):
On fait tourner le cercle d'équation y² + z² = R² autour de l'axe de z
L'axe Oz perce le plan de base de la calotte pour z = R.cos(alpha) = R/2
V1 = Pi * S(de R/2 à R) y².dz = Pi * S(de R/2 à R) (R² - z²).dz = Pi * [R²x - z³/3](de R/2 à R) = Pi*(R³ - R³/3 - R²R/2 + R³/24) = (5/24).Pi.R³
Volume du cône : (supposé non connu)
On fait tourner la droite z = y * tan(90°-alpha), soit z = (1/V3).y autour de l'axe Oz avec z compris entre 0 et R/2
V2 = Pi * S(de0àR/2) y² dz = Pi * S(de0àR/2) 3.z² dz = Pi * [3 * z³/3](de0àR/2) = (1/8).Pi * R³
---
V = V1 + V2 = (5/24).Pi.R³ + (1/8).Pi.R³
V = (1/3).Pi.R³
Sauf distraction. 
Je pense également que c'est ce qu'on devrait trouver (j'ai trouvé ce résultat en utilisant les formules usuelles du volume d'un cône et d'une calotte sphérique) mais lorsque j'intègre au lieu d'un tiers j'obtiens
=
et j'ai toujours le facteur moins du dz.
Et pour le moment d'inertie ?
Compte tenu de l'indication fournie par ton professeur, la méthode attendue pour le volume de la calotte est sans doute celle-ci :
La tranche de cote z et d'épaisseur dz a pour rayon :
et pour épaisseur
.
son volume est :
D'où le volume de la calotte :
Attention aux bornes d'intégration ! mon expression de dV suppose dz>0 donc une intégration de  =
= à
à  =0 !
=0 !
Non je n'y avait du tout pensé, je vais refaire mes calculs avec cette formule car je pense que mon moment d'inertie est faux du coup,
Je pense que oui !
Donc si je comprends bien la formule permet de calculer le volume de la calotte mais pas celui du cône??
Pour le moment d'inertie je crois avoir fait une erreur dans les bornes d' intégration de dx et dy:
Dois-je intégrer dx et dy de 0 à ou de -
à
?
Donc si je comprends bien la formule permet de calculer le volume de la calotte mais pas celui du cône
Je ne pense pas qu'il existe une formule unique pour déterminer le volume du solide ou son centre de gravité ou son moment d'inertie : il faut passer par la décomposition du solide en deux comme cela a déjà été fait pour le volume et la masse. Cela dit, la méthode que je t'ai proposée s'applique très simplement au cône : il suffit de considérer dans le calcul
 comme une constante égale à
comme une constante égale à  .
.
Selon moi, l'expression du moment d'inertie en fonction de R et
 fait intervenir
fait intervenir  . Tu peux expliquer ta méthode ?
. Tu peux expliquer ta méthode ?
Je connais deux théorèmes de Guldin : un qui permet de déterminer le centre d'inertie d'une distribution filiforme de matière, l'autre qui permet de déterminer le centre d'inertie d'une distribution surfacique de matière mais je ne connais pas celui permettant d'obtenir le centre d'inertie d'une distribution volumique de matière...
En fait je pense avoir fait une erreur en intégrant dz 0 à R comme si il ne varie pas du coup j'ai sorti R .
Je pensais que le deuxième théorème de Guldin fonctionnait si on avait la surface et le volume d'un objet mais c'est vrai que je ne comprenais pas bien les résultats du cours entre autre pourquoi quand on intègre un quart de disque on a le volume d'un demi-cercle... du coup je ne sais pas trop comment trouvé le centre d'inertie :/
Ce que tu as déterminé par le théorème de Guldin, sauf erreur de calcul de ta part, c'est la position du centre d'inertie d'une plaque plane constituée d'une partie triangulaire isocèle et d'un demi disque.
Voici une méthode possible pour le moment d'inertie, sachant que celui d'un disque homogène d'axe (Oz) de masse m et de rayon r vaut : IOz=½ mr2
Moment d'inertie du cône par rapport à l'axe (Oz) :
Pour une tranche de cote z et d'épaisseur dz :
la masse est :
le moment d'inertie élémentaire vaut :
On obtient le moment d'inertie du cône en intégrant par rapport à z entre z = 0 et
Moment d'inertie de la calotte par rapport à (Oz) :
La tranche de cote z et d'épaisseur dz a pour rayon :
et pour épaisseur .
son volume est :
Moment d'inertie élémentaire de la tranche :
D'où le moment d'inertie obtenu par intégration :
Le moment d'inertie du solide {calotte + cône) par rapport à (Oz) est donc :
Pour la cote du point G il faut revenir à la formule de définition où tu peux diviser numérateur et dénominateur par  puisque le solide est homogène :
puisque le solide est homogène :
Le calcul intégral, comme dans les deux autres déterminations, se divise en deux : une intégrale pour la partie conique, une autre pour la calotte.
la méthode que je t'ai proposée est physiquement très simple. La difficulté vient des calculs d'intégrales... Je pense qu'un jour d'examen, celles-ci seront fournies...
Bonsoir,
Je propose une solution au calcul de zG avant de passer à autre chose. J'espère que Grenadine75 aura le temps de le refaire. Il s'agit donc de calculer l'intégrale de z.dV sur l'ensemble du solide. Comme, pour les calculs précédents, on procède en deux étapes.
Calcul pour le cône. On a déjà démontré , pour une tranche d'épaisseur ; donc :
Calcul pour la calotte. On a déjà démontré, pour une tranche d'épaisseur et :
;
Pour une fois, le calcul intégral est immédiat puisque : . On obtient :
La somme des deux intégrales vaut : . D'où la cote du centre d'inertie du solide{cône+calotte} :
Ou ainsi pour zG :
Pour la calotte pleine : S(de R/2 à R) [Pi.Rho.z.(R²-z²) dz] = (9/64).Pi.Rho.R^4
Pour le Cône : S(de0àR/2) Pi.Rho.y² dz = S(de0àR/2) Pi.Rho.3.z² dz = (3/64).Pi.Rho.R^4
Total = (12/64).Pi.Rho.R^4 = (3/16).Pi.Rho.R^4
---
Masse = Pi.Rho * [S(de R/2 à R) (R²-z²)dz + S(de 0 à R/2) 3.z² dz] = Pi.Rho.R³/3
--> OG = (3/16).Pi.Rho.R^4/(Pi.Rho.R³/3) = 9R/16
zG = 9R/16
Même résultat que vanoise ...

Bonjour,
Même résultat que vanoise ...
Merci de la confirmation. Et pour le moment d'inertie ?
Pour le moment d'inertie autour de Oz.
Pour la partie conique
Elément de masse : cylindre "creux" d'axe oz, de le rayon y et d'épaisseur de paroi dy et de hauteur (R/2 - z)
La génératrice dans le plan oyz a pour équation z = y/V3
dm = 2.Pi.Rho.y(R/2 - z) dy
dm = 2.Pi.Rho.V3.z.(R/2 - z) V3.dz
dm = 6.Pi.Rho.z.(R/2 - z) dz
J1 = S(de0 à R/2) 6.Pi.Rho.z.(R/2 - z) * y² dz
J1 = S(de0 à R/2) 18.Pi.Rho.z.(R/2 - z) * z² dz
J1 = 18.Pi.Rho.S(de0 à R/2) (R/2.z³ - z^4) dz
J1 = 18.Pi.Rho.[R/8 . z^4 - z^5/5](de0 à R/2)
J1 = 18.Pi.Rho.[R/8 . R^4/16 - R^5/160]
J1 = (9/320).Pi.Rho.R^5
-----
Pour la partie calotte, on peut procéder de la même manière ...
mais en remplaçant l'équation z = y/V3 par l'équation z = V(R²-y²)
Et en intégrant de (R/2 à R)
...

Pour la partie calotte, on peut procéder de la même manière ...
J'aimerais voir si possible, histoire d'être sûr de ne pas m'être trompé dans mon calcul de l'autre soir et histoire que grenadine 75 soit en mesure de comparer les deux méthodes...
Merci d'avance.
Pour le calotte :
dV = 2Pi.y.dy.(z - R/2)
ave x²+y²=R² -->
dV = 2Pi.V(R²-z²)*z/V(R²-z²) * (z-R/2) dz
dV = 2.Pi.(z²-zR/2) dz
dm = 2.Pi.Rho.(z²-zR/2) dz
J2 = 2.Pi.Rho.S(deR/2 à R) (z²-zR/2) * y² dz
J2 = 2.Pi.Rho.S(deR/2 à R) (z²-zR/2) * (R²-z²) dz
J2 = 2.Pi.Rho.S(deR/2 à R) (R²z² - z^4 - R³z/2 + Rz³/2) dz
J2 = 2.Pi.Rho.[R²z³/3 - z^5/5 - R³z²/4 + Rz^4/8](de R/2 à R)
J2 = Pi.rho.R^5 * 53/960
Conforme à la réponse de vanoise.

Bonsoir merci,
Merci à vous J-P et plus particulièrement vanoise pour m'avoir aider à répondre aux questions  j'ai vais bien entendu refaire les raisonnement de mon coté pour comprendre les méthodes de calculs car pour l'instant cela me semble assez long surtout que la colle ne dure qu' une heure. Vanoise ce sujet a été posé lors du concours de deug national de l'an dernier et il n'y avait pas les méthodes sur le sujet... ça me laisse à présager le niveau des épreuves :/
j'ai vais bien entendu refaire les raisonnement de mon coté pour comprendre les méthodes de calculs car pour l'instant cela me semble assez long surtout que la colle ne dure qu' une heure. Vanoise ce sujet a été posé lors du concours de deug national de l'an dernier et il n'y avait pas les méthodes sur le sujet... ça me laisse à présager le niveau des épreuves :/
Encore merci et bonne soirée 
OK : les deux méthodes sont bien cohérentes. Chacun utilise la méthode qui lui est la plus familière. Je pense tout de même que, pour un solide qui, comme ici, admet un axe de symétrie, l'usage des coordonnées cylindriques (ou cylindro-polaires : les expressions sont synonymes) rend les intégrales plus faciles à poser que l'usage des coordonnées cartésiennes. Restent ensuite à résoudre les intégrales : c'est là que, en général, pour ne pas transformer l'épreuve de physique en épreuve de math, un formulaire de primitives est fourni. Cela se fait couramment aux épreuves d'entrée à polytechnique ; pourquoi pas ici ?
Cela d'autant plus que le problème n'est sans doute pas fini : très souvent, ce solide modélise une toupie et il s'agit ensuite de décrire le mouvement de l'axe Oz par rapport au sol lorsque la toupie tourne rapidement sur elle-même autour de cet axe Oz... Et là : il s'agit bien de faire de la physique !


