Inscription / Connexion Nouveau Sujet
Centre d'inertie
Bonsoir j'ai du mal à trouver le centre d'inertie du volume en pièce jointe ou du moins je ne trouve pas mon résultat cohérent :
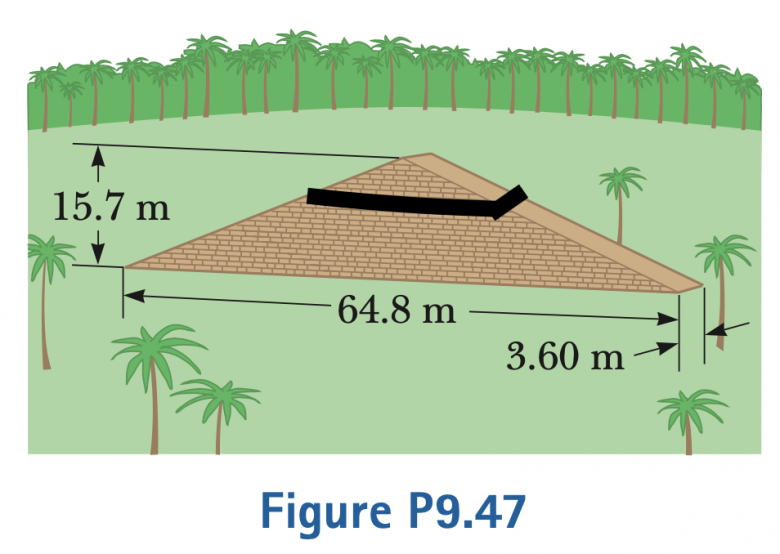
On s'intéresse à la coordonnée selon l'axe des ordonnées du centre d'inertie du volume sur l'image. (Je la nomme yCM). Le volume est formé de milliers de blocs d'une masse volumique égale à d= 3 800 kg/m3. Le volume de masse M est en forme d'un triangle isocèle de base a = 64,8m et faisant b= 15,7m de haut pour une épaisseur de t = 3,60m.
Je fais la chose suivante :
On divise le triangle en bande horizontales de hauteur dy et de longueur x. La masse de chaque bande est le produit du volume de la bande et de la densité : dm = d * x * t * dy = .
On sait de plus que yCM = .
Pour aller plus loin et évaluer l'intégrale, il faut exprimer x en fonction de y. Ici pour tout y compris entre 0 et 15,7 il est facile de montrer que x = a - a/b * y.
yCM = .
En remplacant avec les valeurs numériques, j'obtiens un résultat négatif ce qui n'est pas cohérent malheureusement, quelqu'un pourrait-il m'aider ?
Bonsoir
Ton axe des y est vertical et on note b la hauteur si j'ai bien compris.
Il faut alors intégrer suivant y de 0 à b en explicitant la masse dm de la bande de largeur dy en fonction de dy,y et des paramètres fournis.
Remarque complémentaire : ton calcul se ramène à déterminer le centre d'inertie d'un triangle. Tu connais depuis très longtemps le résultat...
OUI QUELLE ERREUR JE VIENS DE REMARQUER !!!!
Tout se simplifie directement et on obtient b/3.
Faites-vous allusion au centre de gravité du triangle ? Quel lien a-t-il avec le centre de gravité ?
Quel lien a-t-il avec le centre de gravité ?
Dans les cas où les dimensions du système étudié sont suffisamment faible devant le rayon de la terre pour qu'on puisse considérer que le vecteur champ de pesanteur