Bonsoir
Le document que je t'ai indiqué récemment répond à un certain nombre de ces questions. Peux-tu être plus précis sur tes difficultés  ?

Quelques indications en attendant.
Question 1 : tu peux évoquer le diviseur de tension mais il est évident que ve2=vg1 si l'impédance de sortie est infinie (i=0). Evidemment, il y a conservation de la tension mais pas de transmission de puissance.
Question 2 : OK
Pour l'étude du filtre : il s'agit du très classique filtre passe-bande de Wien . Il est commode, pour l'étude du gain, de faire apparaître une constante réelle au numérateur et un "1" au dénominateur en divisant tous les terme par 3jRC. Tu arrives simplement à :


Le gain est le module de H ; le comportement asymptotique qu'on te demande d'étudier va te conduire à vérifier qu'il s'agit bien d'un passe-bande.
Pour la valeur efficace de la tension de sortie (partie 2.2), tu connais sans doute le théorème de Parceval et ses conséquences sur la valeur efficace d'un signal périodique.
Pour l'ampli. op. tu peux consulter le document suivant. Je doute que les démonstrations de la partie II soient à ton programme. Dans un premier temps, tu peux te limiter aux parties I et III.

Bonsoir, merci.

J'ai beaucoup de mal a comprendre ce qu'est la valeur efficace du signale en entrée et  le gain en valeur efficace.

Le gain du filtre pour un signal d'entrée sinusoïdal est le rapport des valeurs efficaces des tensions.  C'est aussi le rapport des amplitudes des tensions. C'est le module de la fonction de transfert indiquée dans mon dernier message.  Pour un signal d'entrée périodique quelconque, on détermine la tension de sortie pour chacune des composantes sinusoïdales de la décomposition de Fourrier puis on applique le théorème de Parceval pour obtenir la tension efficace de sortie.

Avec les notations du paragraphe 2.1 :

tu connais depuis longtemps l'expression de la valeur efficace en fonction de l'amplitude pour un signal sinusoïdal. La démonstration est fournie dans le document précédent que je t'ai fourni et elle est rappelée dans ce TP :



En sortie, le signal est toujours sinusoïdal ; il y a donc le même rapport entre amplitude en sortie et valeur efficace en sortie. Le gain en valeur efficace est donc égal au gain en valeur efficace pour un signal sinusoïdal ; sa valeur est le module de la fonction de transfert :



Cela va te permettre d'étudier le comportement du filtre pour une tension sinusoïdale.

Pour le paragraphe 2.2 : appliquer le théorème de Parseval, comme déjà expliqué.

Je te laisse faire des propositions...

Petit lapsus dans mon message précédent ; il faut lire :
"Le gain en valeur efficace est donc égal au gain en amplitude pour un signal sinusoïdal "

Bonjour, merci beaucoup pour vos reponse ca m'a bien aidé.

en ecrivant la fonction de transfert comme vous je trouve un gain nul lorsque f tend vers 0 et l'infini et un gain de 1/3 pour f=fo.  j'ai donc Vs=1/3 *Ve ce qui donne Veff=1/3 Ve eff. en faisant le rapport de Vs eff et Ve eff je trouve bien 1/3.

Pour la 2.2 je ne comprend pas sur quoi appliqué le theoreme de perseval. La serie de fourier ne suufit pas ?


Pour l'aop je suis désolé mais meme avec votre document je ne comprend pas comment calcule le gain.

merci

OK pour 2.1
Pour 2.2 : Il s'agit juste d'établir l'expression de la valeur efficace d'un signal carré non alternatif. Pour la composante alternative du signal : la valeur efficace se calcule en faisant la moyenne du carré de la valeur instantanée. Or : que peut-on dire de la valeur du carré d'une tension carrée ? Le résultat est immédiat (aucun calcul) et ne demande pas l'usage de l'analyse de Fourier.
Tu obtiens au final la valeur efficace de la tension carrée non efficace par le théorème de Parseval :



et comme déjà dit, l'expression de se déduit de façon immédiate de la valeur de .

La question suivante sur les séries de Fourier est déconnectée de ce qui précède et n'est qu'une application directe de l'annexe A en fin de document.
Pour 2.3, franchement, sans cours préalable structurée sur l'ampli op... Enfin bon...
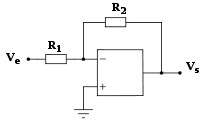
Il s'agit d'étudier le circuit ci-dessous avec R1=Rp et R2=(1-)Rp.
Liaison par résistance entre E- et S en absence de liaison entre E+ et S : l'ampli op fonctionne en régime linéaire ; V(E+)=V(E-) .
V(E+)=0 entrée non inverseuse reliée à la masse
Théorème de Millman appliquée à l'entrée inverseuse :




Je ne détaille pas : tout est sur le document que je t'ai fourni.

Bonsoir, merci beaucoup.