Inscription / Connexion Nouveau Sujet
Caractérisation de défauts à partir d'une source thermique
Bonjour à tous,
Je participe à un projet visant à caractériser des défauts dans des matériaux composites en dynamique.
Pour ce faire, je dispose de plusieurs échantillons, d'une caméra thermique (IR), une barre chauffante et un banc d'essai munit d'un chariot mobile.
Les échantillons de matériaux composites sont placés horizontalement sur le banc et la caméra thermique est placé au-dessus de ces échantillons.
La caméra est fixé au chariot mobile, tout comme la barre chauffante.
Vous trouverez un schéma pour illustrer la manipulation.
La problématique est la suivante :
étude d'optimisation du couple vitesse d'avancement et puissance de chauffe, pour un delta T en surface (Tchaud - T froid (initial)) d'environ 10 °C max . Puis 5°C puis 15°C.
Je n'ai pas beaucoup de notion en transfert thermique..
Mais j'imagine que nous avons cette situation jointe. Si jamais ce n'est pas le cas, corrigez-moi.
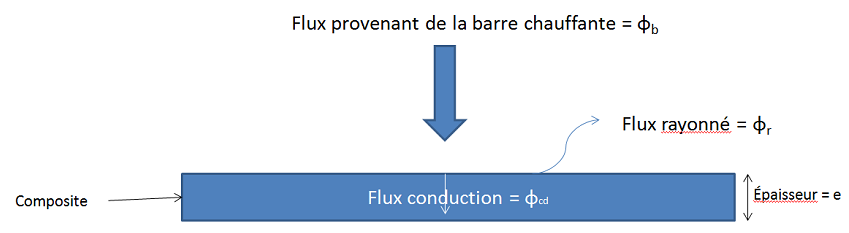
On serait donc face au flux suivant :
Q_b=hS?T
Q_cd=-k?TS
Q_r= ?ST^4 ?
Je ne vois pas trop comment intégrer la vitesse de déplacement du chariot et la puissance de chauffe de la barre.
Pouvez-vous m'aiguiller ?
Faut-il passer par le nombre de Reynolds pour faire apparaitre la vitesse ?
Re = ( 
 Vm
Vm ]L) /
]L) /
et Ensuite passer par le Nu et le Pr ?
Je vous remercie par avance pour votre aide et votre compréhension,
Respectueusement,
3inge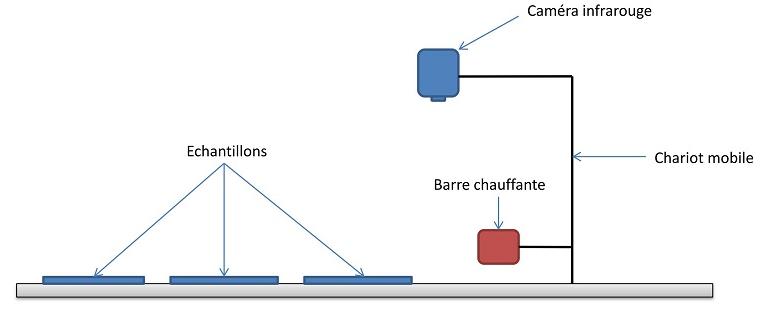
***Images recadrées***
Bonjour
À priori, je ne vois pas trop ce que le nombre de Reynolds vient faire ici. Les transferts thermiques sont en général relativement lents. L'aérodynamisme de la partie mobile importe sans doute assez peu. Il s'agit sans doute plutôt d'optimiser la vitesse pour que le passage de la barre chauffante produise une élévation de température ayant l'ordre de grandeur souhaité. Cela passe par un bilan des flux thermiques reçus et perdus par l'échantillon,par rayonnement et conduction - convention, en fonction de la position de la barre. Connaissant la masse et la capacité thermique massique de l'échantillon, il sera alors possible de modéliser l'augmentation de température.
Réflexions fournies sans la moindre garantie : je n'ai pas une vision globale du projet.
Remarque : grâce à une sonde thermique et une carte d'acquisition reliée à un pc, il est peut être possible d'enregistrer les variations de température au cours du temps pour différentes positions de la barre chauffante...
Tout d'abord merci beaucoup pour votre réponse complète Vanoise 
Pour le bilan thermique, dois-je prendre en compte deux dimensions ? de manière à prendre en compte la profondeur de chauffe dans l'échantillon et la position de la barre au dessus de l'échantillon.
Concernant, la modélisation de l'augmentation de température pas connaissance de la masse et de la capacité thermique massique de l'échantillon,
Pouvez-vous m'en dire davantage ? Existe-il une formule particulière comprenant ses deux paramètres et les reliant à la température ?
Respectueusement,
3inge
Bonsoir
Si la longueur de la barre chauffante est nettement supérieure à la largeur de l'échantillon, je crois que le flux thermique transmis par la barre à l'échantillon ne dépend que d'un seul paramètre de position de la barre, son abscisse par exemple.
Si tu notes Pth la somme algébrique des flux thermiques reçus par l'échantillon, t le temps, T la température, m et c la masse et la capacité thermique massique de l'échantillon :
Pth. dt =m.c. dT soit : dT /dt =Pth /m.c
Ceci n'est valide que si l'échantillon est suffisamment bon conducteur thermique et pas trop long pour qu'il soit possible de considérer que la température T de l'échantillon ne dépend que de t et pas de l'abscisse... Dans le cas contraire il faut faire le bilan sur une tranche élémentaire d'échantillon. Plus compliqué...
A nouveau, merci beaucoup pour votre réponse 
L'échantillon possède une largeur de 24cm et la barre de chauffe une longueur de 79 cm.
Le rapport semble-t-il suffisant pour pouvoir considérer ce cas de figure ?
Respectueusement,
3inge
Concernant Pth la somme des flux reçues par l'échantillon.
Dois-je prendre en compte la puissance délivrée par la barre et la conduction au sein de l'échantillon ? ou la puissance délivrée par la barre seul ?
Respectueusement,
3inge
Rapport longueur barre sur largeur échantillon largement suffisant. Quelle est la longueur de l'échantillon ? Importante sans doute. Dans ce cas, impossible de considérer T comme uniforme dans l'échantillon. Quel est son épaisseur?
Surtout : quelle est la finalité de l'expérience?
la longueur de l'échantillon est de 40 cm,
l'épaisseur est de 3cm,
Le but est de pouvoir caractériser les défauts présent dans l'échantillon.
Il est donc nécessaire que l'échantillon soit exposé suffisamment longtemps à la puissance reçue, afin que la chaleur puisse se propager suffisamment en profondeur afin d'atteindre les défauts.
Il serait donc intéressant de pouvoir estimer ce temps d'exposition en fonction de la puissance.
Bonjour
grâce à une sonde thermique et une carte d'acquisition reliée à un pc, il est peut- être possible d'enregistrer les variations de température au cours du temps pour différentes positions de la barre chauffante...
Tu ne m'as pas répondu sur ce point. Cette expérience serait intéressante car ton problème dépend d'un grand nombre de constantes dont les ordres de grandeur vont être difficiles à connaître : coefficient de réflexion de la surface de l'échantillon concernant le rayonnement émis par la barre ; conductivité thermique de l'échantillon...
La puissance thermique émise par la barre est a priori constituée d'un terme due au rayonnement et d'un terme due à la conduction-convection. Le premier est peut-être prépondérant ??? Cela dépend entre autre de la température de la barre.
Bref : tout cela est TRÈS compliqué. Une expérience permettant d'évaluer l'augmentation de température en fonction du temps en divers points de l'échantillon pour une position fixe de la barre permettrait d'y voir beaucoup plus clair.
Je ne suis pas du tout spécialiste des matériaux composites ; aussi, je ne vois pas vraiment comment un défaut en profondeur modifierait le rayonnement infrarouge émis...
Bonjour,
Veuillez m'excuser pour cette non-réponse,
On ne peut placer de sondes dans nos échantillons, le but est de faire un contrôle non-destructif afin de pouvoir contrôler des structures du génie civil.
Les défauts présent dans les composites montent plus en température que le reste de l'échantillon, on peut donc les observer, je vous joint une photo d'un échantillon chauffé, image capturée avec une caméra infrarouge.
nous avons déjà les variations de température de nos échantillons en fonction du temps, nous avons enregistrer en temps réelle des séquences de chauffe et de refroidissement de nos échantillons, et à partir de ces séquences nous pouvons extraire les signaux temporels en différentes positions.
En fait je cherche plutôt à expliciter ce phénomène sur papier, bilan thermique, formule mathématique appliquée, et comparé la théorie avec les résultats obtenus.

Bonjour
Je commence à comprendre... Imaginons un défaut en profondeur moins bon conducteur thermique que le reste de l'échantillon. La puissance thermique transmise verticalement au socle par conduction sera plus faible à la verticale de ce défaut : la température de surface à la verticale du défaut sera plus élevée et donc détectable par la caméra. Je peux tenter une modélisation très simplifiée : je me place en régime quasi permanent. L'approximation n'est pas excellente mais sinon, il faudrait résoudre des équations différentielles faisant intervenir le laplacien de la température... J'isole une petite portion cylindrique de l'échantillon, d'axe vertical, de hauteur H= 3cm (hauteur de l'échantillon) et de base d'aire S.
Le flux thermique (puissance thermique) fournie par la barre vaut : où PS représente la puissance absorbée par unité de surface.
Une partie de cette puissance est rayonnée vers l'extérieur conformément à la loi de Stéphan : où TS représente la température de surface et
la constante de Stéphan.
Une partie de cette puissance est cédée à l'air ambiant par convection conformément à la loi de Newton : où h est la constante de Newton et Ta la température ambiante.
Une autre partie de cette puissance est cédée par conduction au socle situé sous l'échantillon et supposé à la température Ta :
où Rth est la résistance thermique et
la conductance thermique de l'échantillon supposé pour l'instant sans défaut.
Toujours dans l'hypothèse du régime quasi permanent, le bilan thermique conduit à :
soit, après simplification :
avec :  =5.67.10-8USI ;
=5.67.10-8USI ;  =0,2USI ; h=10USI ; Ta=293K ; TS=298K , on obtient : PS=530W/m2
=0,2USI ; h=10USI ; Ta=293K ; TS=298K , on obtient : PS=530W/m2
Supposons maintenant le même cylindre, recevant la même puissance surfacique, et contenant un défaut d'épaisseur e = 2mm de conductivité thermique égale au dizième de celle de l'échantillon sans défaut. La nouvelle résistance thermique vaut :
La température de surface est maintenant solution de l'équation :
Une résolution numérique conduit à une température de surface égale à : 298,62K; Je pense qu'un écart de 0,62K par rapport à la température moyenne de surface est détectable par une telle caméra.
Les valeurs numériques que j'ai choisies ne correspondent sans doute pas à ton échantillon. A toi d'adapter si nécessaire...
J'aurais dû mieux me relire : il s'agit de la conductivité thermique, comme d'ailleurs, je l'ai écrit quelques lignes plus bas...
La conductance thermique est l'inverse de la résistance thermique, par analogie avec le vocabulaire utilisé en électrocinétique.
Bonjour Vanoise,
Excusez moi de ne répondre que maintenant, j'ai atterri au Québec entre temps^^ toujours dans le cadre de l'avancement de mon projet.
Merci beaucoup cette explication c'est beaucoup plus claire ! 
Je vais regarder ça de mon côté et je reviens vers vous si besoin.
Je vous remercie sincèrement pour votre aide.
3inge
Bonjour Vanoise,
En discutant avec mes partenaires de projets, on a conclu que cette première approche permettait de bien comprendre le problème.
Cependant lors de nos expérience on chauffe pendant un temps fini, il serai donc intéressant d'essayer d'intégrer le temps dans cette modélisation.
Où doit-on modifier ce modèle ? au niveau de la conduction ?
Faudrait-il partir de l'expression de la conduction en régime dynamique ?
Je vous remercie par avance pour votre aide,
Respectueusement,
3inge
Bonjour
Faudrait-il partir de l'expression de la conduction en régime dynamique ?
J'ai déjà évoqué ce problème : ma modélisation est simpliste puisqu'elle utilise l'approximation du régime quasi permanent. En toute rigueur, il faudrait effectivement intégrer l'équation différentielle de Laplace sur la conservation de l'énergie mais la présence du laplacien ne simplifie pas les choses.
Il y a sans doute un moyen terme : calculer l'énergie que doit recevoir l'échantillon pour passer d'un état initial de température uniforme Ta à un état final où la température de surface est TS=Ta+5 (en kelvins), le profil de température dans l'échantillon étant celui que j'ai déjà décrit. Connaissant la puissance absorbée par l'échantillon quand la barre passe au -dessus de lui, il sera possible de déterminer un ordre de grandeur du temps de passage...
Pour cela, il faut connaître le coefficient d'absorption de l'échantillon, sa capacité thermique massique, sa masse...
En assimilant la barre à une barre cylindrique, il sera même possible d'exprimer cette puissance en fonction de la position de la barre par rapport à l'échantillon pour avoir une expression plus précise du temps de passage.
Peut-on considérer que la barre transmet très majoritairement de l'énergie à l'échantillon sous forme de rayonnement ?
Merci pour votre rapide réponse,
Oui on peut dire que la barre transmet très majoritairement de l'énergie à l'échantillon sous forme de rayonnement.
Oui on peut dire que la barre transmet très majoritairement de l'énergie à l'échantillon sous forme de rayonnement.
Voilà une bonne nouvelle. En assimilant la barre à un cylindre, la puissance reçue par une surface élémentaire de largeur l = 24cm et de longueur élémentaire dx, située à la distance r de l'axe de la barre peut s'écrire :
où
 désigne l'angle entre la verticale et la droite passant par l'élément de surface étudié et l'axe de la barre et où K désigne une constante dépendant de la puissance totale émise par la barre et du coefficient d'absorption de l'échantillon (peut-être pas évident à déterminer...)
désigne l'angle entre la verticale et la droite passant par l'élément de surface étudié et l'axe de la barre et où K désigne une constante dépendant de la puissance totale émise par la barre et du coefficient d'absorption de l'échantillon (peut-être pas évident à déterminer...)
Pour un mouvement de la barre par rapport à l'échantillon connu au cours du temps, r et
 sont des expressions faciles à exprimer en fonction du temps. Par intégration, Il sera ainsi facile de déterminer l'énergie fournie à l'échantillon en fonction de la vitesse de la barre. Seule gros problème pour moi : comment obtenir le coefficient d'absorption ou le coefficient de réflexion...
sont des expressions faciles à exprimer en fonction du temps. Par intégration, Il sera ainsi facile de déterminer l'énergie fournie à l'échantillon en fonction de la vitesse de la barre. Seule gros problème pour moi : comment obtenir le coefficient d'absorption ou le coefficient de réflexion...Si l'on connait les valeurs des coefficients d'absorption, est-ce toujours un problème ?
les échantillons dont on dispose sont des échantillons aux propriétés connues.
Si le coefficient d'absorption est connu, il suffit d'écrire que la puissance absorbée est le produit de la puissance reçue par rayonnement par le coefficient d'absorption. En toute rigueur, ce coefficient varie en fonction de  mais, pour obtenir un ordre de grandeur, on peut sans doute le considérer comme une constante.
mais, pour obtenir un ordre de grandeur, on peut sans doute le considérer comme une constante.
Une rapide intégration de l'expression précédente montre que l'énergie absorbée par une bande d'échantillon de largeur l et de longueur dx vaut :
où h est la distance entre la face supérieure de l'échantillon et la trajectoire du centre de la barre et où V est la vitesse de translation de la barre.
Si on note L = 40cm la longueur de l'échantillon, en négligeant la puissance absorbée par les faces verticales de l'échantillon, on obtient une énergie totale absorbée :
Ce résultat parait intuitivement assez logique : l'énergie reçue est proportionnelle à l'aire L.l de la face supérieure de l'échantillon. De surcroît, plus la barre passe loin de l'échantillon et plus elle passe vite, plus l'énergie reçue est faible... Reste à exprimer K.
Essaie de faire la démonstration...
Calcule ensuite l'énergie nécessaire pour atteindre le profil de température désiré ; en identifiant, tu obtiendras un ordre de grandeur de la vitesse V...
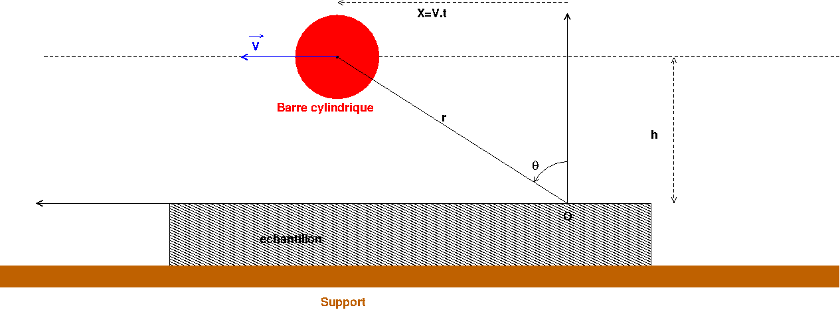
Réflexion faite, je ne sais pas si tu vas pouvoir te sortir de la démonstration... Voici un schéma représentant la barre à un instant quelconque lors de son mouvement. On s'intéresse à la puissance absorbée à la date t par une bande élémentaire de largeur l et de longueur élémentaire dx centrée au point O.
L'énergie élémentaire absorbée par la tranche élémentaire entre t et (t+dt) a pour expression :
On peut supposer que la barre chauffante part de suffisamment loin vers la droite pour aller suffisamment loin sur la gauche pour qu'il soit possible d'intégrer entre -90° et 90° ; l'énergie absorbée par la tranche élémentaire est ainsi :
Pour avoir ensuite l'énergie absorbée par toute la face supérieure de l'échantillon il suffit d'intégrer sur la longueur de celui-ci :
Merci pour cette réponse complète, je vais essayer de faire la démonstration
l'expression :
http://latex.ilephysique.net/ile_TEX.cgi?dU=\frac{2K\cdot%20l}{h\cdot%20V}\cdot%20dx
découle de celle-ci : http://latex.ilephysique.net/ile_TEX.cgi?\boxed{dP=K\cdot\frac{l\cdot\cos\left(\theta\right)}{r^{2}}dx}
?
Bonjour Vanoise,
Est-il possible d'accéder à la température de surface avec cette dernière formule ?
Avec :
Dans une première approche : oui. En régime quasi permanent, la variation de T en fonction de la profondeur z dans l'échantillon étant une fonction affine, tu peux calculer la variation d'énergie interne en prenant :
 T=(TS-Ta)/2, la température moyenne dans l'échantillon étant passée de Ta à (TS+Ta)/2
T=(TS-Ta)/2, la température moyenne dans l'échantillon étant passée de Ta à (TS+Ta)/2
Compte tenu de la difficulté à déterminer K sans faire d'expérience, cette approche est peut-être suffisante. Sinon tu peux tenter un peu plus sophistiqué en considérant que toute l'énergie fournie par la barre à l'échantillon n'est pas intégralement convertie en énergie interne, une partie est perdue par rayonnement, une autre par convection dans l'air, une autre par conduction dans le support.
Compte tenu de la difficulté à déterminer K sans faire d'expérience
Le constructeur de la barre chauffante fournit peut-être la valeur de l'intensité énergétique rayonnée : Ir, c'est à dire de la puissance rayonnée par unité d'angle solide (unité : le watt par stéradian). Puisque la barre n'est pas cylindrique, cette intensité dépend peut-être de l'angle
 . Cette dépendance modifierait un peu le calcul précédent mais pas de façon insurmontable.
. Cette dépendance modifierait un peu le calcul précédent mais pas de façon insurmontable.
Il suffirait alors de poser : K= Ir.A avec A : coefficient d'absorption de l'échantillon...



