Inscription / Connexion Nouveau Sujet
Calculs de Matrice d'Inertie
Bonjour, en ce moment je m'entraine sur le calcul de matrice d'inertie, mais je bloque sur le cône...
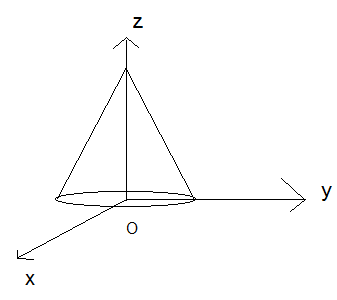
Le rayon de la base du cône est R et la hauteur du cône est H, la masse volumique ρ est homogène dans tout le cône.
Je voudrais calculer la matrice d'inertie du cône au point O.
Les produits d'inerties sont tous nul car le solide admet deux plans de symétrie (xOz) et (yOz).
De plus le solide possède une symétrie de révolution selon l'axe z.
On aura une matrice d'inertie du cône de la forme :
Pour la valeur de JB, je bloque, j'ai fais :
dJB = ρ (x²+y²) dV
Or :
dV =  R²(z) dz =
R²(z) dz =  R²(1 - z/h)² dz
R²(1 - z/h)² dz
Et :
r² =  0R
0R  0R dx dy
0R dx dy
Alors :
dV = R²(1 - z/h)²  0R
0R  0R dx dy dz
0R dx dy dz
Donc :
dJB = ρ (x²+y²) R²(1 - z/h)²  0R
0R  0R dx dy dz.
0R dx dy dz.
JB = R²ρ 0h (1 - z/h)² dz
0h (1 - z/h)² dz  0R
0R  0R (x²+y²) dx dy
0R (x²+y²) dx dy
= 2/3 M R²
C'est faux, je devrais trouver 3/10 M R²... Pourriez-vous m'aider à trouver mon erreur merci.
Apparemment il faut utiliser les coordonnées cylindrique, j'ai vu un exemple avec le cylindre et je retrouve le bon résultat.
Mais maintenant le truc que je ne comprend pas c'est que pourquoi on aurait :
dV = r dr dθ dz


