Inscription / Connexion Nouveau Sujet
Calculer i(t)
Bonjour, j'ai un problème pour le calcul de i(t) dans R pour les deux schémas ci-joint
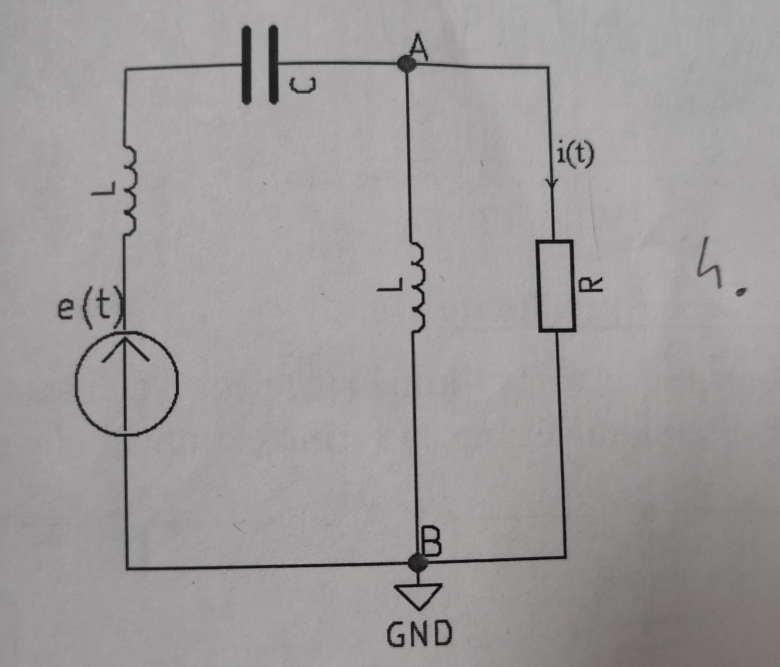
Dans le schéma que j'ai numéroté 4, pour obtenir i(t) j'effectue la loi des mailles avec avoir préalablement calculer Thevenin entre A et B
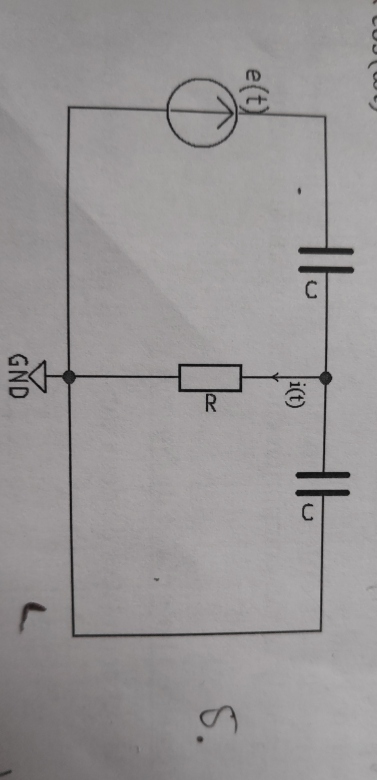
Dans le schéma numéroté 5, pour obtenir le résultat attendu je commence par faire Millman mais ensuite je ne peux pas faire la lois des mailles mais je dois utiliser U=R.I
Pourquoi les méthodes pour trouver i(t) ne sont pas les mêmes ? Comment savoir quel méthode utilisé a quel moment ?
Bonjour
Tu ne précises pas l'expression de e(t). S'agit-il d'étudier le circuit en régime sinusoïdal établi ? Si oui, il faut raisonner à partir des complexes associés en utilisant la méthode que tu as indiquée puis revenir aux valeurs instantanées.
J'ignore quel est ton niveau pour ce type de problème. A tout hasard, tu trouveras ici les bases, partie 1 essentiellement :
![]()
Dans le schéma 4 on ne nous donne pas de valeur de e(t), dans le 5 e(t)=E0.cos(wt)
Oui aucun problème avec les complexes et valeurs instantanée mais je ne comprends pas pourquoi dans un cas on utilise la lois des mailles et dans l'autre seulement la loi d'ohm
Pour les deux circuits, tu peux déterminer la tension aux bornes de R par le théorème de Millman puis appliquer la loi d'Ohm à R. Pour le circuit 4, la tension entre A et B est la tension commune aux trois branches :
1° : R
2° : L
3° : e +L+C (association série)
D'accord donc j'aurai aussi pu utiliser Millman pour la 4
Donc en conclusion lorsque l'on utilise Millman il suffit de faire une loi d'Ohm avec la résistance en question pour obtenir i(t)
Mais lorsque l'on fait Thevenin ou Norton on doit passer par une loi des mailles
C'est ca ?
Donc en conclusion lorsque l'on utilise Millman il suffit de faire une loi d'Ohm avec la résistance en question pour obtenir i(t)
oui si la tension U obtenue par le théorème de Millman est la tension aux bornes d'une résistance.
L'utilisation du théorème de Thévenin ou de Norton est différente : tu commences par rechercher les caractéristiques du circuit une fois la résistance R débranchée puis tu rebranches la résistance pour obtenir l'intensité du courant qui la traverse. De mon point de vue (mais chacun a ses habitudes...), cette méthode est à réserver aux circuits plus complexes que ceux étudiés ici.
Ma question est peut être un peu bête mais dans quel cas la tension obtenu avec Millman n'est pas aux bornes d'une résistance ?
Où plutôt, comment sais t-on que la tension obtenu avec Millman est la tension aux bornes de la résistance ?
Reprends le circuit 4. La tension UAB déterminée par le théorème de Millman est la tension aux bornes de R mais c'est aussi la tension aux bornes de L et c'est aussi la tension aux bornes de l'association série {générateur, bobine,condensateur}.
Autre réponse possible : dans le circuit 4, remplace R par un dipôle quelconque d'impédance Z. Le théorème de Millman sera toujours applicable entre A et B pour trouver la tension commune UAB aux trois branches.


