Inscription / Connexion Nouveau Sujet
calcul travail
Bonsoir,
Je cherche à déterminer l'équation du mouvement du pendule simple à l'aide du théorème de l'énergie cinétique.
De ce fait: 
Ec= 
W
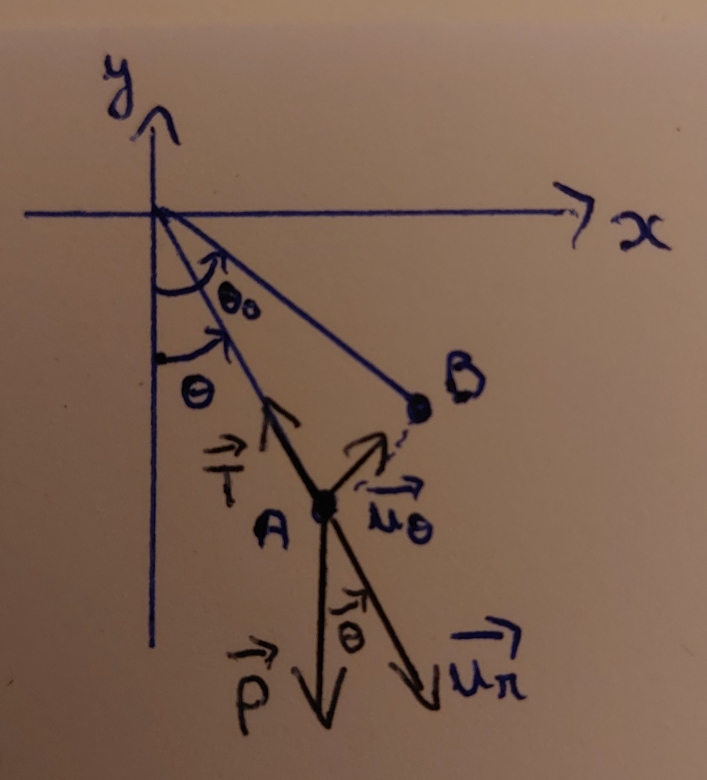
Je prends 2 points A et B afin d'appliquer le théorème de l'energie cinétique entre ces points.
Je choisis A qui fait un angle 
quelconque entre la verticale et le fil rejoignant la masse au point A. Et je choisis B de telle manière à ce que sa vitesse soit nulle et donc que sont énergie cinétique soit nulle.
Je peux écrire Ec= (1/2)ml2w2 avec w=d/dt
Calcul du travail:
Méthode 1:
W=
W
Il y 2 forces extérieures appliquées à la masse: P et T
La tension du fil ne travaille pas car à tout moment la tension du fil est orthogonale (sur l'axe de ur) au déplacement (sur l'axe de uo).
W= (mgcos ur-mgsin u) . (ld u) = -mgsin ldo
J'intègre de à 0 pour ytouver le travail:
W = mgl (cos0 -cos)
W=(équation 1)
On dérive le théorème de l'énergie cinétique par rapport au temps et on retrouve l'équation différentielle du mouvement:
d2/dt2 + g/l sin =0
Méthode 2:
W=F.L=F*L*cos(P,L)
F=mg, L=l(0-), cos(P,L)=cos(+
/2)= -sin
Déjà je trouve un travail différent, c'est étrange.
Je dérive par rapport au temps et je trouve:
d2/dt2 + g/l sin + g/l cos =0
Alors mes questions:
1/Pourquoi on ne résout pas l'équation différentielle de l'équation 1 ? Parce que c'est une équation différentielle non linéaire et on ne sait pas la résoudre ?
2/Quelle est la signification physique de la dérivée dans ce cas là ?
Ça a la dimension d'une puissance donc la puissance cinétique égale à la puissance du déplacement ?
3/ Pourquoi la methode 2 ne fonctionne pas ?
Merci d'avance
Bonsoir
1/Pourquoi on ne résout pas l'équation différentielle de l'équation 1 ? Parce que c'est une équation différentielle non linéaire et on ne sait pas la résoudre ?
sin(
)
2/Quelle est la signification physique de la dérivée dans ce cas là ?
De quelle dérivée parles-tu ?
3/ Pourquoi la methode 2 ne fonctionne pas ?
Tu utilises une formule du travail valide seulement pour une force de vecteur constant (c'est bien le cas) lorsque le point d'application de la force se déplace rectilignement, ce qui n'est pas le cas...
1/ mgl(cos0-cos)=(1/2) m l2(d/dt)2
Soit (d/dt)2 +(2g/l) (cos - cos 0) = 0
Si on apprime cos 1 (et pourquoi pas les termes suivants), on ne pourrait toujours pas résoudre l'équation différentielle parce qu'il y a un carré à d/dt ou il y a une méthode permettant de la résoudre ?
2/ La dérivée du théorème de l'énergie cinétique par rapport au temps soit:
dEc/dt = dW/dt
3/ Ah d'accord, c'est valable que pour des déplacent rectiligne mais vu que W=F.dl si F est constant, je peux le sortir de l'intégrale/le mettre en facteur et du coup juste calculer dl et après ce calcul je fais ce produit scalaire ?
Ou vu que quand dans l'équation de W, F et dl doivent être dans le même repère, cartésien ou polaire, et dans ce cas, ils ne sont plus constants et donc je dois d'abord faire le produit scalaire avant d'intégrer ?
Pour la 1/ , après l'approximation:
On voit l'identité remarquable a2-b² = (a-b)(a+b) donc l'équation différentielle est résoluble ?
Sauf si on va plus loin dans le développement limité
Question 1 : aux amplitudes faibles, un développement limité au second ordre des cosinus conduit à :
D'où l'équation différentielle :
On dérive par rapport au temps :
Sachant que la vitesse angulaire n'est pas nulle au cours du mouvement, tu obtiens la même équation différentielles pour les faibles amplitudes que par l'autre méthode.
Question 2 : Dériver par rapport au temps l'expression du théorème de l'énergie cinétique conduit à ce que les ”mécaniciens” appellent le théorème de l'énergie-puissance :
où p(t) désigne la puissance instantanée de toutes les forces appliquées au système.
Question 3 : si tu projettes le vecteur déplacement suivant la verticale puisque la seule force qui travaille est le poids, tu vas aboutir à l'équation différentielle que tu rappelles en début de message.
D'accord, ça devient plus clair.
Comment choisir l'ordre du développement limité, notamment ici pour le cosinus: il s'agit parce qu'il y a premièrement (d/dt)² ou parce qu'on obtient une équation différentielle du second ordre que l'on se limite au DL au 2nd ordre ? et pourquoi pas à l'ordre 0 ou à l'ordre 1 ?
Et pourquoi nous ne résolvons pas directement l'équation différentielle ici du théorème de l'énergie cinétique ou par exemple de l'énergie mécanique ?
On pose w=
g/l
On a (d/dt)² + w² (²-0²)=0
En utilisant l'identité remarquable (a²-b²)=(a+b)(a-b)
On peut écrire : d/dt + w (²-0²)1/2 =0
Et, d/dt - w (²-0²)1/2 =0
Ces équations différentielles ne sont pas résolubles à cause de la racine carré sur la fonction qui rend l'équation non linéaire ou c'est résoluble ?
Alors on dérive par rapport au temps pour enlever certaines constantes du systèmes qui empêchait la bonne résolution de l'équation différentielle ?
La méthode que tu proposes dans ton dernier message n'aboutit à rien. Il faut commencer par dérivée par rapport au temps comme expliqué précédemment.
En revanche, la méthode est utilisée pour obtenir la période des oscillations mais là encore : rien de bien simple : on obtient la période comme égale à une intégrale qu'il n'est possible de résoudre que numériquement. Si cela t'intéresse d'approfondir un peu, tu peux consulter cette fiche à partir du paragraphe III.3. Le reste concerne l'étude de balanciers d'horloges...
Annuler
connectez vous