Inscription / Connexion Nouveau Sujet
Calcul tensions simple etoile triphasé sans neutre
Bonjour,
J'ai un problème à résoudre qui consiste à déduire (ou calculer) les tensions simples d'un générateur triphasé couplé en étoile sans neutre connaissant uniquement les tensions mesurées aux bornes des charges de chacune des 3 branches.
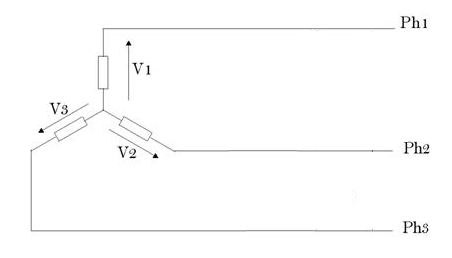
Voici un schéma, ce sera plus simple.
Les tensions V1, V2 et V3 sont connues car elles sont mesurées en temps réel par un dispositif de mesure électronique. De ces tensions nous devons déduire la valeur des phases PH1, PH2 et PH3.
Pour information, il s'agit d'un système électronique qui est censé mesurer l'amplitude des phases PH1, PH2 et PH3.
Bonjour ,
les relations sont données au chapitre 4 http://fr.wikipedia.org/wiki/Courant_triphas%C3%A9
Cordialement
Bonjour et merci pour ta réponse.
Cependant l'article wiki ne répond pas à ma question. D'une part l'article décrit un cas équilibré et fait appel aux tensions composée.
Hors mon système est potentiellement déséquilibré et les tensions simples PH1/N, PH2/N et PH3/N que je cherche à calculer sont référencées par rapport au N alors que les tensions que je mesure sont référencées par rapport au point central de l'étoile.
En claire à partir de ces dernières tensions je dois trouver une équation qui me permette de calculer les tensions simples PH1/N, PH2/N et PH3/N.
(je me demande si c'est possible!)
Sous quelles formes sont donnés V1 , V2 et V3 ?
On fait :
U(Ph1 Ph2) = V2 - V1
U(Ph2 Ph3) = V2 - V3
U(Ph3 Ph1) = V3 - V1
Bien, entendu, V1, V2 et V3 doivent être donnés soit sous formes vectorielles, soit sous formes complexes, soit autrement mais avec possibilité de retouver les amplitudes et les déphasages entre ces différentes tensions.
-----
Sauf distraction. 
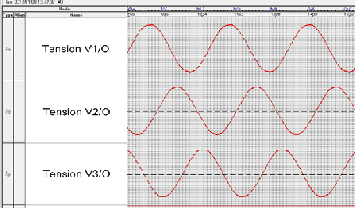
En fait les tensions V1,V2 et V3 sont échantillonnées en temps réel par un FPGA via 3 convertisseur A/N dont la référence de tension est le point centre de l'étoile (qu'on appellera 'O'). Donc ces tensions ont comme référence ce point central. Ci-dessous une copie d'écran des échantillons acquis par le FPGA (un outil de debug embarqué dans le FPGA permet d'avoir cette représentation temporelle des échantillons).
Après on en fait ce qu'on veut sur le plan du calcul.
Alors effectivement je peux appliquer ton calcul sauf que ce que je cherche c'est pas les tensions composées (U Ph1 Ph2) mais les tensions simples PH1, PH2 et PH3 évidemment référencées par rapport au neutre. C'est un peu la que ca se complique il me semble. En clair je cherche une équation du type : Ph1/N = f(V1/O,V2/O,V3/O) idem pour Ph2 et Ph3.
En principe , le centre de l'étoile correspond au neutre . Si ce n'est pas le cas , il faut préciser où est le neutre .
Effectivement dans mon cas le neutre n'arrive pas sur le point milieu de l'étoile (ce point est flottant). Le neutre sert de référence aux phases PH1, PH2 et PH3.
Quand les phases PH1, PH2 et PH3 sont équilibrées, le calcul de leur valeur à partir des mesures faites sur V1,V2 et V3 est facile. PH1 =V1 etc.. Le problème se pose lorsque les phases PHx ne sont plus équilibrées (PH1 différente des autres phases par exemple).
Et bien c'est alors assez simple :
Dans mon message précédent, lire :
U(Ph1 Ph2) = V2 - V1
U(Ph2 Ph3) = V3 - V2
U(Ph3 Ph1) = V1 - V3
On lit sur les diagrammes et on déduit :
V1 = V1max.sin(wt)
V2 = V2max.sin(wt + Phi1)
V3 = V3max.sin(wt + Phi2)
V1max, V2max, V3 max, Phi1 et Phi2 sont mesurés à partir des diagrammes.
Et on calcule :
U(Ph1 Ph2) = V2 - V1
U(Ph1 Ph2) = V2max.sin(wt + Phi1) - V1max.sin(wt)
U(Ph1 Ph2) = V2max.sin(wt + Phi1) - V1max.sin(wt)
...
**********
Dans le cas présent, il semble que V1max = V2max = V3max
et si je lis bien que Phi1 = -2Pi/3 et Ph2 = -4Pi/3
On a donc à faire à 3 tensions de même amplitude et déphasées de 2Pi/3
Cela signifie que les charges sont équilibrées.
Le réseau est donc triphasé avec les tensions entre phase d'amplitude = V1max
et V1 max est connu (puisque mesurable sur le graphique).
On peut le calculer bien que ce soit inutile dans le cas présent.
En effet :
U(Ph1 Ph2) = V2max.sin(wt + Phi2) - V1max.sin(wt)
U(Ph1 Ph2) =V1max.[sin(wt - 2Pi/3) - sin(wt)]
...
U(Ph1 Ph2) = Racine(3) * V1max.sin(wt - 5Pi/6)
de manière analogue, on calcule :
U(Ph2 Ph3) = V3 - V2
U(Ph2 Ph3) = V1max.(sin(wt - 4Pi/3) - sin(wt - 2Pi/3))
...
U(Ph2 Ph3) = Racine(3) * V1max.sin(wt + Pi/2)
U(Ph3 Ph1) = V1 - V3
U(Ph3 Ph1) = V1max.(sin(wt) - sin(wt- 4Pi/3))
...
U(Ph3 Ph1) = Racine(3) * V1max.sin(wt - Pi/6)
on a donc :
U(Ph1 Ph2) = Racine(3) * V1max.sin(wt - 5Pi/6)
U(Ph2 Ph3) = Racine(3) * V1max.sin(wt + Pi/2)
U(Ph3 Ph1) = Racine(3) * V1max.sin(wt - Pi/6)
ces 3 tensions sont triphasées (même amplitudes et décalage de +/- 2Pi/3 entre ces 3 tensions)
Dans le cas du graphique donné, le noeud de l'étoile des charges est au même potentiel que le neutre du réseau triphasé.
Et donc les potentiels des phases par rapport au neutre sont les V1, V2 et V3 du schéma.
-----
Evidemment, avec d'autres graphiques, les calculs sont similaires ... et peuvent aboutir à montrer que le noeud de l'étoile n'est pas au même potentiel que le neutre.
C'est ce qui arriverait si les charges n'étaient pas équilibrées avec le noeud de l'étoile non raccordé au neutre.
Dommage de faire un tel exercice dans le cas particulier de charges équilibrées.
-----
Sauf distraction. 

Merci pour cette belle démonstration. Mais effectivement ce cas équilibré ne pose pas de problème.
C'est le cas ou les tension PH1, PH2, PH3 ne sont pas équilibrée qui me pose problème.
Si tu veux ce système a pour objet de surveiller un générateur triphasé. Donc l'idée est de faire des mesures sur des résistances en étoile (fixes et égales) d'où les valeurs mesurées V1,V2 et V3 et d'en déduire pas le calcul les phases PH1,PH2,PH3 surtout quand il y a un problème au niveau du générateur, à savoir qu'il génère des tensions non équilibrées. Donc moi c'est plutôt ce cas de "dysfonctionnement" qui m'intéresse et de pouvoir dire attention la phase PH2 par exemple est à 35V au lieu des 100V nominal.
On fait le même genre de calculs mais avec les vraies valeurs mesurées sur les diagrammes de V1max, V2max, V3 max, Phi1 et Phi2
Exemple si on a :
V1 = 400.sin(314.t)
V2 = 381.sin(314.t - 2) (ici 2 est en radian)
V3 = 402.sin(314.t - 2,1) ici 2 est en radian)
On calcule U(Ph1 Ph2) = V2 - V1
U(Ph1 Ph2) = 381.sin(314.t - 2) - 400.sin(314.t)
Par calculs ... ou bien par n'importe quels autres moyens :
U(Ph1 Ph2) = 656,2 * sin(314t - 2,585)
On fait le même genre de manipulations pour calculer :
U(Ph2 Ph3) et U(Ph3 Ph1)
Et on peut alors comparer les 3 tensions en amplitude et en phase.
Mais ce n'est évidemment valable qu'au moment où les mesures (éléborations des 3 graphiques) sont faites.
---
Mais ici, on ne peut pas calculer par rapport au neutre du réseau.
Par contre on peut directement faire des mesures de tension entre le neutre du réseau (en supposant qu'il est disponible à l'endroit de la mesure) et le point commun de l'étoile des charges.



