Inscription / Connexion Nouveau Sujet
calcul résistance équivalente
Bonjour,
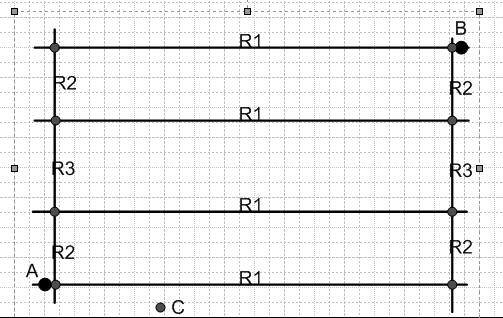
Je cherche à calculer la résistante équivalente au réseau suivant entre les points A et B.
Les barres horizontales et transversales sont reliées entre elles par des résistances de valeur C. Les autres résistances R1 à R3 sont indiquées dans le schéma.
Pourriez-vous m'aider SVP ?
D'avance merci.
Bonjour baltoche,
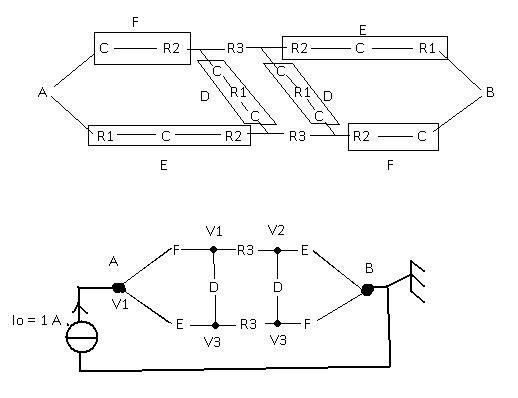
Je me suis permis de retravailler ton dessin pour rendre les choses plus claires : voir premier dessin !
Pour simplifier, je regroupe les résistances en séries :
D=R1+2C
F=C+R2
E=R1+R2+C
On obtient ainsi un circuit électrique déjà plus simple (pour moi en tout cas  ).
).
Le fait est que le circuit n'est plus réductible car il n'y a plus de résistance en série ou en parallèle !
J'applique à l'ensemble des résistances un courant Io (tu peut oublier le "=1A" ça sert pas au final), et je relie B à la masse. L'objectif est maintenant de déterminer la tension entre les point A et B, càd déterminer le potentiel Va (/!\ erreur  : remplacer le premier V1 à gauche par Va, dsl)
: remplacer le premier V1 à gauche par Va, dsl)
En effet : Va=Req*Io <=> Req=Va/Io avec Req étant la résistance équivalente !
Je préconise d'utiliser la loi des nœuds aux points associés aux potentiels V1,V2,V3,V4 et évidemment Va.
On obtient 5 équations pour 5 inconnues (V1,V2,V3,V4,Va), le première étant :
Io+(V1-Va)/F+(V3-Va)/E=0 <=> Va*(F+E)-V1*E-V3*F=F*E*Io (1)
Les 4 autres équations te permettent d'exprimer V1,V2,V3,V4 en fonction de Va.
Tu obtient ainsi à partir de (1) une équation de la forme : Va=k*Io (k résistance inconnue s'exprimant en fonction de C,R1,R2,R3).
Avec k=Va/Io=Req, donc c'est gagné  (normalement)
(normalement)
Les calculs sont longs, pas difficiles mais avec beaucoup de possibilités de se tromper ...
Je te laisse le soin de les faire, bon courage 
"Bonus" : j'ai pensé au départ à utiliser des propriétés de symétrie du circuit (symétrie centrale) pour simplifier, mais apparemment seules les symétries par rapport à un plan de symétrie (ou d'antisymétrie) sont valides... donc pas de simplification possible au final 
Bonsoir Dimith,
Quelle réactivité, merci !
Merci d'avoir pris la peine de t'être penché sur mon problème. Pour ta culture, j'ai ainsi modélisé un ferraillage d'acier sous une voie ferrée, et dans lequel je cherche à calculer les courants vagabonds, i.e. issus du rail et allant corroder les structures métalliques enterrées.
Je suis parfaitement d'accord avec ton premier schéma (c'est important car toute la suite en dépend).
Tu me suggères 5 équations à 5 onconnues. Excel aurait très bien géré cela en matrices, mais j'ai besoin des expressions littérales (démonstration à faire au client. En plus c'est à Dubaï donc je ne te dis pas l'exigence de mon interlocuteur !). Je vais donc me "palucher" les calculs, car je n'ai pas bien le choix. comem tu le dis, ce n'est pas dur mais c'est facile de se tromper.
A vue d'oeil, je serais prêt à dire que le courant dans les deux résistances "E" est le même. On a en effet, sauf erreur de ma part, une anti-symétrie par rapport au plan joignant les milieux de chacun des R3. d'après la théorie, on serait donc en meusre de tirer une équipotentielle entre ces deus points, et peut-être de simplifier le circuit ? A vérifier...
L'avantage avec les outils de simulation numérique est que je pourrai au moins vérifier mes formules littérales, par exemple en faisant R3=E=F, le circuit tombant alors dans des cas classiques de quadripoles.
Bref, la balle est dans mon camp maintenant, à la lumière de tes efforts pour lesquels je te remercie.
Très bonne soirée,
Baltoche.
Bonsoir baltoche  ,
,
Concernant l'antisymétrie apparente : on ne peut a priori pas tirer de conclusion (même si c'est très tentant) car l'antisymétrie doit résider dans le fait d'avoir une symétrie du montage par rapport à l'axe mais d'avoir un même sens pour le courant à de par et d'autre de l'axe. Ici, la symétrie du montage n'est pas respectée.
Peut-être que ton intuition est juste, mais il n'y a pas (encore) de règle général permettant d'aboutir à ce résultat  .
.
Je vais essayer de me frotter aux calculs :
point de potentiel Va : Va*(F+E)-V1*E-V3*F=F*E*Io (A) (/!\ j'ai changé le nom de cette éq pour pas se mélanger)
point de potentiel V1 : (Va-V1)/F+(V3-V1)/D+(V2-V1)/R3=0 <=> V1*(R3*D+R3*F+F*D)=R3*D*Va+R3*F*V3+F*D*V2 (1)
point de potentiel V2 : (V1-V2)/R3+(V4-V2)/D+(-V2)/E=0 <=> V2*(R3*D+R3*E+D*E)=D*E*V1+R3*E*V4 (2)
point de potentiel V3 : (Va-V3)/E+(V1-V3)/D+(V4-V3)/R3=0 <=> V3*(R3*D+R3*E+D*E)=D*E*V4+R3*E*V1+R3*D*Va (3)
point de potentiel V4 : (V3-V4)/R3+(V2-V4)/D+(-V4)/F=0 <=> V4*(R3*D+R3*F+F*D)=R3*F*V2+F*D*V3 (4)
J'obtiens par la "magie" de l'informatique  (logiciel: Maple 5):
(logiciel: Maple 5):
V4 = 1/2*Io*F*(2*E+D)/(F+E+D), V2 = 1/2*Io*E*(D+2*F)/(F+E+D), V1 = 1/2*Io*(R3*F+R3*D+D*E+R3*E+2*F*E)/(F+E+D), V3 = 1/2*(R3*D+F*D+R3*F+R3*E+2*F*E)*Io/(F+E+D)
Va = 1/2*(R3*D+F*D+D*E+R3*F+R3*E+4*F*E)*Io/(F+E+D)
Ainsi on obtient une résistance équivalente : Req=1/2*(R3*D+F*D+D*E+R3*F+R3*E+4*F*E)/(F+E+D)
Ce qui est déjà homogène à une résistance (ouf!).
On développe les groupes D,E,F, ce qui donne après quelques minutes de concentration :
Je t'ai même fait un Latex pour l'occasion 
J'espère qu'il s'agit du bon résultat (tu vas sûrement reprendre les calculs pour vérifier, on sait jamais  ).
).
On remarque aussi que ton intuition\ta règle était juste  : V1-V2=V3-V4 mais je n'ai pas voulu prendre de risques (peut-être est-ce un cas particulier, ou je suis juste neuneu
: V1-V2=V3-V4 mais je n'ai pas voulu prendre de risques (peut-être est-ce un cas particulier, ou je suis juste neuneu  ).
).
Je pressens déjà la suite avec n barreau au lieu des 4 de l'exercice  mais ça sera intéressant
mais ça sera intéressant 
Je te souhaite bonne chance pour ton projet 
Hello Dimith,
Non seumlement tu me donnes des tuyaux mais en plus tu fais le boulot (en fouettant to ordi) pour moi. Que demander de plus ??? je te rassure, je ne demanderai pas le même exercice avec un nombre variable de barreaux !).
Je fais confiance à Mapple (au fait, je ne connais pas. Que fais de beau ce logiciel, car ça pourrait me servir dans mes modélisations), et demain, dans l'avion, je mettrai toutes les résistances à la même valeur et je verrai si la formule littérale a du sens (en plus d'être homogène).
Comme tu le soulignes, j'ai vu une anti-symétrie là où il n'y en avait pas (j'ai vu ce que je voulais y voir...), la règle de V1-V2=V3-V4 me paraissait trop belle pour être... fausse. Cela dit, la prudence s'impose car une mauvaise hypothèse au départ fait passer des heures de calcul pour rien.
Demain donc, je pense valider tes résultats, mais j'ai très confiance !
Merci à toi, c'est chic de ta part. Alstom t'en remercie également... même s'ils ne le savent pas.
Si cela t'amuse, j'ai un autre exercice de même type avec réseaux de résistances (je cherche à modéliser des équipotentielles de rail).
En te souhaitant une bonne journée...
A bientôt,
Baltoche


