Inscription / Connexion Nouveau Sujet
calcul de la résultante de la force de pression
Bonjour, et meilleur voeux a tous
je bloque sur cette exercice et un coup de neurone me serai salvateur,
Un aquarium rempli d'eau a raz bord contient des poissons exotique.
Un hublot de rayon 40Cm permet d'observer les poissons.
Ce hublo est situe a une distance e=20Cm de la surface libre du fluide.
Question
Calculer et situer le point d'application des forces de pression subit par le hublot
Ma méthode:
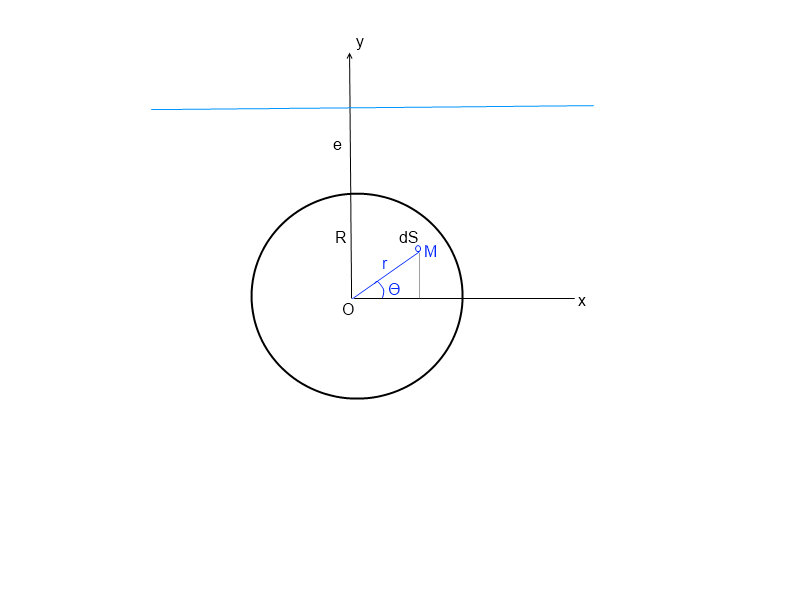
Je situe mon repere voir schema
Pour calculer la force pressante je pose
V


ensuite je pose l'equation du cercle par rapport a mon repere
2
2
2
j'exprime donc par rapport a
ensuite je remplace dans la force pressante et je trouve
V



2
2
Voila a partir de la je suis bloqué et en plus j'ai un doute sur les borne de mon intégrale
en tenant compte de mon repère je doute s'il faut prendre entre ou entre
Si vous pouvez m'éclaircir sur les borne a prendre
Mon blocage viens du fait que je n'arrive pas a transformer en
Deja si vous m'aider a trouver la force pressante et les borne d'intégration je pourrais calculer le point d'application
Cordialement a tous et merci davance pour votre aide
bonsoir,
on te demande le centre de poussée, pas la résultante
de plus je pense qu'il faut plutôt essayer en coordonnées polaires pour faciliter l'intégration
Bonsoir,
oui on me demande le centre de poussée mais dans la formule
du calcul du centre de poussée tu as la force résultante qui est interviens
ce qui a mon sens est quand même logique
d'ou ma démarche de la calculer au préalable.
Au cas ou vous auriez une méthode qui se passe de la force résultante
je vous remercie d'avance
Cordialement
comme le hublot est circulaire je ferais l'intégration en polaires.
en M:
 P = rho g (e+R - r sin O)
P = rho g (e+R - r sin O)
dF =  P dS = rho g (e+R - r sin O) r dr dO (dirigé selon Oz)
P dS = rho g (e+R - r sin O) r dr dO (dirigé selon Oz)
la résultante se calcule en calculant: F = 
 disque dF
disque dF
et pour le centre de poussée C on remarque qu'il est sur Oy pour des raisons de symétrie, donc on cherche h = OC
vérifiant Mo (forces de pression) = h F = 
 disque OM ^ dF
disque OM ^ dF
ou encore h F = 
 disque r dF
disque r dF
sauf erreur
OK je vous remercie déjà de m'accorder de votre précieuse attention
Visiblement vous ouvrez une voie dont je ni songeais pas du tout néanmoins je pense
qu'elle compréhensible pour le commun des mortel.
Je tiens cependant a avoir quelque éclaircissement SVP
EN On a



ca je suis d'accord




alors la je ne comprend pas d'où sort le devant

et
Mo (forces de pression) = h F =

 disque OM ^ dF
disque OM ^ dFaussi Mo comme vous dites force de pression =hF ce serait FS ?
et quelle serait les bornes de vos integrale ?
j'ai deja pense a explote la symetrie
Cordialement
en polaires l'élément infinitésimal de surface en m(r;O) est: dS = r dr dO ![]()
(ça ne peut pas être dr dO car dr dO n'est pas homogène à une surface!)
le disque est bien la surface du hublot
si C est le centre de poussée
le moment en O des forces de pression est: Mo = OC ^ F
et c'est aussi: Mo = 
 D OM ^ dF
D OM ^ dF
d'où
OC ^ F = 
 D OM ^ dF
D OM ^ dF
ce qui permet de trouver C (qui doit être sur Oy)
si on pose: C(xC,yc) on a: xc=0 yc= OR
OR  O2
O2 r sin O dF
r sin O dF
sauf erreur
Bonsoir; Krinn pouvez vous m aider svp a résoudre l'exercice suivant:![]() Mouvement Relatif?
Mouvement Relatif?
Bonsoir 
Je vais reprendre l'exercice avec la methode que vous m'avez expliquer et je vous tiens au courant de ce que je trouve
Merci encore





Sans rentrer dans les détails(sauf si besoin est?), alors moi je trouve
yc=-32 (évidemment je m'attendais à une réponse négative sinon ça aurait pas été logique)
Quand à F je trouve F=10053,01N est ce pas énorme pour un aquarium de quelque centimètre ?
lol c'est pas un aquarium de mercure de l'eau donc je suis un perplexe
oups :o
:o :o
:o petit couac
petit couac
heuu Krinn en appliquant la formule sur Yc je trouve -r^2 soit -0,16 et 0,16<20 donc le centre
de poussée est hors du cercle est ce logique ?
bonsoir,
dF = rho g (e+R - r sin O) r dr dO
je pose k = e+R
F =  oR
oR  o2
o2 dF
dF
=  g [
g [  oR
oR  o2
o2 k r dr dO -
k r dr dO -  oR
oR  o2
o2 r2 sin O dr dO ]
r2 sin O dr dO ]
= 
 gk R2
gk R2
OC ^ F = 
 D OM ^ dF (égalité vectorielle)
D OM ^ dF (égalité vectorielle)
d'où : xc=0 (par symétrie)
F yc = 
 D r sin O dF = -
D r sin O dF = - 
 g R4/4
g R4/4
donc yc = -R2/(4(e+R))
sauf erreur
Bonjour,
dsl de reagir aussi tardivement.
Alor deja je te remerci pour tte l'aide que tu m'as apporté jusqu'ici 
Alor pour revenir au sujet moi j'ai developpoé une autre methode et je d=tombe sur le meme
resultat que toi a G près.
alors ma demarche et la tienne on trouve la meme force resultante soit
pour le centre de poussé moi j'ai y
alors que toi t'as
y=
ce qui me semble pas tres logique car dans ce cas notre centre de poussée se situerai hors du cercle. Alors est ce que tu te serai pas trompé ?
est ce que ton expression qui donne
- g*pi*rho R^4/4
et une petite remarque si t'ajoute Zg stadire (e+r) a ton expression alors toi et moi trouvons la meme chose
merci de bien vouloir me faire un retour
Cordialement
= je trouve: yc = OC = -0.42/4/0.6 = -0.067 m = - 6.7 cm
ce qui me paraît cohérent
(dans mon repère (O,x,y), O correspond au centre du hublot, donc C est 6.7 cm en-dessous de O ce qui ne me paraît pas aberrant)




