Inscription / Connexion Nouveau Sujet
Calcul de déphasage
Salut tout le monde,
S'il vous plait je trouve souvent des difficultés en ce qui concerne le calcule de déphasage .. J'ai une méthode directe dans le cours -Mais que j'arrive pas à bien comprendre ! - :
La mesure de déphasage d'un signal 2 par rapport à un signal 1 s'effectue ainsi :
1)On prend un instant de référence t1 sur le signal 1 (parce qu'on s'intéresse au déphasage du signal 2 par rapport au signal 1). Il peut s'agir par exemple d'un instant où le signal est maximum ou minimum.
2)On cherche un instant analogue t2 sur le signal 2. Par exemple, si vous avez choisi un maximum comme point de référence, il vous faut un maximum. Attention, il ne faut pas choisir n'importe quel instant analogue, mais celui le plus près de votre instant de référence. Il s'agit d'une convention qui revient à considérer le déphasage comme compris entre −π et π.
3)On mesure le retard Δt 2/1 du signal 2 par rapport au signal 1, défini par Δt 2/1= t2 - t1 .
4)On en déduit le déphasage grâce à la formule :
Δt 2/1= =2πfΔφ 2/1=2πf(φ2-φ1) .
Cette méthode donne directement le déphasage entre les deux signaux, sans passer par les phases à l'origine.
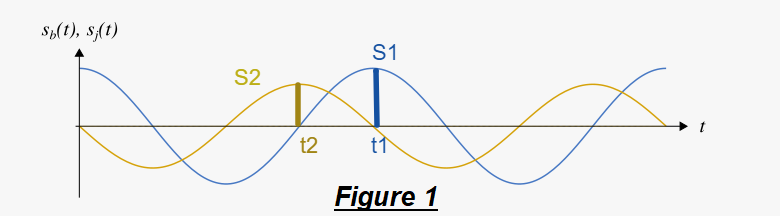
J'ai essayer d'appliquer cette méthode sur S1=A1.cos(
 t+φ1) et S2=A2.cos(
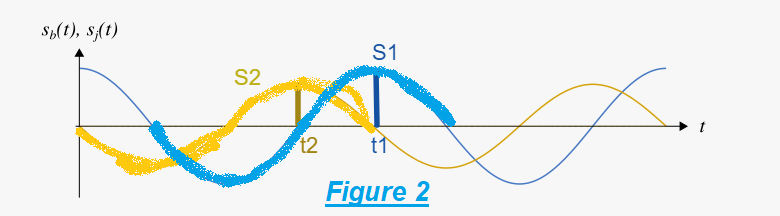
t+φ1) et S2=A2.cos( t+φ2) dans la figure 1 : d'après le schéma C'est S2 qu'est en avance de phase par rapport à S1 . Comment j'ai fait ? J'utilise une "petite astuce" que j'ai représenter dans la Figure 2 : Je représente deux pulsations voisines de S1 et S2, je remarque que c'est S1 qui semble en avance par rapport à S2. Donc c'est le contraire : C'est S2 qu'est en avance de phase par rapport à S1 .
t+φ2) dans la figure 1 : d'après le schéma C'est S2 qu'est en avance de phase par rapport à S1 . Comment j'ai fait ? J'utilise une "petite astuce" que j'ai représenter dans la Figure 2 : Je représente deux pulsations voisines de S1 et S2, je remarque que c'est S1 qui semble en avance par rapport à S2. Donc c'est le contraire : C'est S2 qu'est en avance de phase par rapport à S1 .
Donc Δφ 2/1=φ2-φ1 >0, mais lorsque j'applique la méthode que j'ai en cours ( voir t1 et t2 Figure 1) je trouve que t2-t1<0 donc Δφ 2/1=φ2-φ1 <0 !
Je ne comprend pas d'ou viens la méthode de cours, ni la "petite astuce", c'est pour cela que je trouve souvent des problèmes..
Je vous demande alors s'il vous plait de m'aider à comprendre tout ce qui concerne la phase ..
Merci infiniment a tous les membres su forum

Bonjour,
S2 est bien en avance. Votre astuce fonctionne.
Ma méthode, qui est celle de votre cours, consiste à regarder le passage par zéro montant (ou descendant) et dire que le signal qui y passe le premier est en avance.
Il n'y aurait pas par hasard une faute de frappe dans Δt 2/1=-2πfΔφ 2/1=2πf(φ2-φ1) (perte du moins dans la dernière expression) ?
"Donc Δφ 2/1=φ2-φ1 >0", OKi.
"je trouve que t2-t1<0 donc Δφ 2/1=φ2-φ1 <0 !"
Si vous appliquez votre formule pour Δφ, vous trouvez Δφ>0, donc OK.
Si vous appliquez votre formule pour (φ2-φ1), vous trouvez (φ2-φ1)<0, NON, donc retour à ma question de faute de frappe.
Remarque : le déphasage entre deux signaux a un sens physique (retard/avance), contrairement aux phases à l'origine.
Il est préférable de repérer le passage par zéro, plus précis car la courbe coupe l'axe, on peut même la faire couper l'axe de manière abrupte en jouant sur le calibre vertical. Défaut de la méthode : il faut être sûr du zéro (mode GND pour contrôler la position, puis mode AC) . Au maximum, par définition, le signal change peu, donc le repérage temporel sera imprécis.
Merci beaucoup pour votre réponse,
Je viens de vérifier mon cours, j'ai bien recoupier le texte, ce n'est pas une faute de frappe...
Je peut conclure alors que la bonne relation est : Δt 2/1=(t2-t1)=-2πfΔφ 2/1=2πf(φ1-φ2) ?
Ou bien que c'est : |Δt 2/1|=2πf|Δφ 2/1| , et après je détermine le signe de Δφ2/1 en déterminant si S2 en avance ou en retard de phase par rapport à S1 .. mais c'est plus lourd.
Je n'ai pas bien compris votre méthode
Il est préférable de repérer le passage par zéro
de repérer le passage par zéro
le passage par zéro montant (ou descendant)
Merci infiniment pour vos efforts

Je peux conclure alors que la bonne relation est : Δt 2/1=(t2-t1)=-2πfΔφ 2/1=2πf(φ1-φ2) ?
Cela me parait raisonnable : Δφ 2/1=φ2-φ1
Pour ce qui est du passage par zéro, c'est moi qui ait été un peu elliptique : passage par zéro signifie sb(t)=0 ou s2(t)=0.
mais c'est plus lourd
oui et non : on compte les carreaux ou on demande


