J'ai une autre question Pourquoi est ce que les potentiels s'additionnent (superposition) ?

salut
tu es en fluide parfait ?
sinon il suffit d'appliquer la continuité des vitesses à la paroi

Oui c'est un fluide parfait. Ca n'est pas bon les intégrales ?

ba si mais je ne suis pas sur que ça te serve à quelque chose
pour la vitesse je voterais plutot pour utiliser l'équation d'euler

je suppose qu'on est en stationnaire,
par symétrie on peut supposer que la vitesse est de la forme

Mais on a pas encore fait ça en classe.
En fait, je me suis trompée, on a pas de cylindre, M est représenté par des coordonnées cylindres, mais on a le même écoulement dans tout le plan.
Je ne sais pas justifier que v ne dépend pas des variables d'intégration, un peu comme avec le théorème de Gauss l'an dernier.

donc ton intégrale c'est D = u(r).H.dr  mais on connait pas encore u(r)

je mettrais selon er, non ? puisque l'écoulement est radial.

bon alors réexplique moi correctement le problème stp

oki, je vais faire le schéma sur paint

Le fluide est supposé parfait, l'écoulement permanant, radial de façon homogène. On nous donne le débit volumique Dv. Et il faut calculer v(M)

Mes camarades de classe m'ont dit qu'ils ont trouvé v=Dv/2rp

Mais je ne sais pas comment ils ont justifié leur intégrale

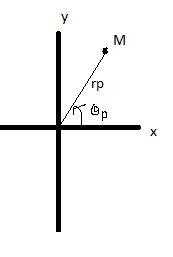
ah un écoulement radial ok je vois c'est facile alors
effectivement v est dirigé selon e_r donc l'élément dS = r.d.dr
l'écoulement est homogène donc v = constante
ici c'est plutot un débit surfacique que volumique (ça se voit aux unités). Donc v sort de l'intégrale et il y a juste à intégrer sur un cercle de rayon rp

ahh, v=cste grace à "homogène"! le truc c'est que comment on sait que ds est également dirig selon er ?

pck l'écoulement est selon er

si tu essaie une autre surface tu vas trouver un flux nul

oui justement c'est pourquoi j'aurai mis er mais à partir de maintenant je sais qu'il faut l'orienter selon l'écoulement !

MERCI !

pour ta question :"J'ai une autre question  Pourquoi est ce que les potentiels s'additionnent (superposition) ?"

il faut savoir que les potentiel sont des variable independantes de quelconques vecteur unitaire, ce sont des vecteur physique,plus communement appelés "vecteur scalaire".
c'est ainsi que nous pouvons dire que le potentiel crée au point M est : V(M)=somme(Vi(M))