Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau autre
Partager :

Calcul d'intensité

Posté par
matix 04-03-11 à 14:28

Bonjour,

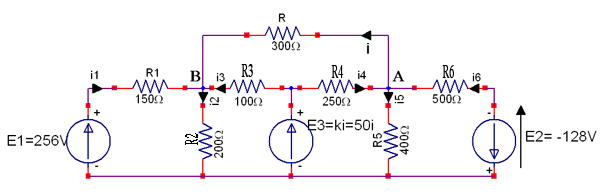
Sur le circuit ci-joint, je cherche à calculer le courant i.. J'ai tenté de le faire en écrivant les 5 lois des mailles possibles, je me retrouve au final avec pas mal de calculs, et tout ça pour obtenir quelque chose de faux à la fin en plus... Voyez-vous une méthode plus rapide ?

Merci d'avance.

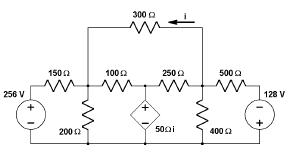
Calcul d\'intensité

Posté par
Marc35re : Calcul d'intensité 04-03-11 à 15:43

Bonjour,
Millman pour trouver VA et VB.
Le courant en découle.

Calcul d\'intensité

Posté par
matixre : Calcul d'intensité 04-03-11 à 15:56

Je souhaiterais ne pas utiliser Millman dans la mesure du possible, on nous le déconseille... Autre chose d'envisageable ? Désolé..

Posté par
Marc35re : Calcul d'intensité 04-03-11 à 16:24

Très efficace, Millman, quand on sait s'en servir...
Théorème de superposition ?

Posté par
matixre : Calcul d'intensité 04-03-11 à 16:26

Pourquoi pas le théorème de superposition oui.. A chaque cas, il faut trouver la résistance équivalente du circuit pour parvenir à i ?

Posté par
Marc35re : Calcul d'intensité 04-03-11 à 18:12

On peut faire Thévenin à chaque extrémité pour simplifier et appliquer ensuite le théorème de superposition.
Mais c'est pas gagné. Le circuit est encore compliqué.

Posté par
matixre : Calcul d'intensité 04-03-11 à 18:57

Finalement, Millman semble la meilleure solution ?

Posté par
Marc35re : Calcul d'intensité 04-03-11 à 20:19

Millman est sûrement la meilleure solution.
Mais je n'arrive pas à bien lire ce qu'il y a sur le générateur du milieu : 50 I ?
Mais que vaut I ?

Posté par
matixre : Calcul d'intensité 05-03-11 à 20:44

50 ohm i : et il faut justement calculer i, que l'on retrouve dans la branche du haut du circuit..

Posté par
Marc35re : Calcul d'intensité 05-03-11 à 23:40

J'ai peut-être une idée mais je crois que ça va être Millman sans le dire...
Il faut que je creuse un peu...

Posté par
Marc35re : Calcul d'intensité 06-03-11 à 12:52

Les potentiels sont mesurés par rapport à la ligne du bas (V = 0).
On a :  i\,=\,\frac{V_A-V_B}{R}
D'après la loi des noeuds, on a :
i_4+i_6\,=\,i_5+i

\frac{ki-V_A}{R_4}\,+\,\frac{E_2-V_A}{R_6}\,=\,\frac{V_A}{R_5}\,+\,i
Que l'on peut écrire :
3$V_A\,=\,\frac{i\left(\frac{k}{R_4}-1\right)+\frac{E_2}{R_6}}{\frac{1}{R_4}+\frac{1}{R_6}+\frac{1}{R_5}}
3$V_B\,=\,\frac{i\left(\frac{k}{R_3}+1\right)+\frac{E_1}{R_1}}{\frac{1}{R_1}+\frac{1}{R_3}+\frac{1}{R_2}}
D'où :
3$V_A-V_B\,=\,R\,i\,=\,\frac{i\left(\frac{k}{R_4}-1\right)+\frac{E_2}{R_6}}{\frac{1}{R_4}+\frac{1}{R_6}+\frac{1}{R_5}}\,-\,\frac{i\left(\frac{k}{R_3}+1\right)+\frac{E_1}{R_1}}{\frac{1}{R_1}+\frac{1}{R_3}+\frac{1}{R_2}}
Que l'on peut écrire :
3$R\,i\,=\,\frac{i(k-R_4)R_6R_5\,+\,R_4R_5E_2}{R_6R_5+R_4R_5+R_4R_6}\,-\,\frac{i(k+R_3)R_1R_2\,+\,R_3R_2E_1}{R_3R_2+R_1R_2+R_1R_3}
Là, il faut peut-être passer à l'application numérique... Cela peut s'arranger pour obtenir quelque chose de la forme a i = b mais cela n'amène pas grand-chose, à part des expressions gigantesques...
Ce n'est pas autre chose que Millman. J'ai redémontré Millman sur un cas particulier en fait.

Sauf erreur de recopie ou autre...

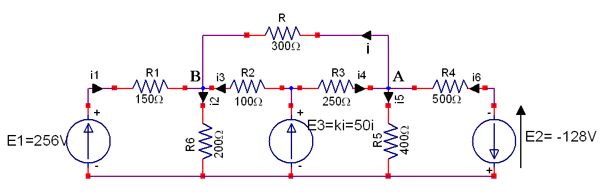
Calcul d\'intensité

Posté par
Marc35re : Calcul d'intensité 06-03-11 à 12:54

Attention au sens que j'ai pris pour E2 !
Avec le sens choisi, E2 = - 128 V

Posté par
matixre : Calcul d'intensité 06-03-11 à 21:39

Merci pour tous ces détails ! Par contre, pour la première loi des noeuds (en A), n'est-ce pas plutôt :

\frac{ki-V_A}{R_3}\,+\,\frac{E_2-V_A}{R_4}\,=\,\frac{V_A}{R_5}\,+\,i ?

Je n'ai pas encore regardé pour la suite.

Posté par
Marc35re : Calcul d'intensité 06-03-11 à 21:54

Désolé, c'est le schéma qui est faux...
Je ne sais pas pourquoi d'ailleurs !...

Calcul d\'intensité

Posté par
matixre : Calcul d'intensité 06-03-11 à 22:15

C'est parfait, je tombe sur le bon résultat ! Merci encore pour toute l'aide apportée.

Bonne soirée !

Posté par
Marc35re : Calcul d'intensité 06-03-11 à 23:43

Parfait


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !