Inscription / Connexion Nouveau Sujet
Calcul d'incertitude
Bonjour, j'ai bientôt un DS d'électricité et il y aura parmi les exercices un calcul d'incertitude.
J'essaye de refaire des sujets des années passées pour réviser mais je n'arrive pas à faire ce genre de calcul, en fait c'est surtout la formule des dérivées partielles que je ne comprends pas vraiment :
 U = (
U = ( U/
U/ X)
X) 
 X + (
X + ( U/
U/ Y)
Y) 
 Y ...
Y ...
Si quelqu'un pouvait m'éclairer sur la façon de procéder 
Merci d'avance 
Il s'agit en fait de la formule générale d'une différentielle. Soit, par exemple U fonction de deux variables indépendantes X et Y. La différentielle de U s'écrit :
Si les erreurs commises sont a priori faibles, on peut assimiler les erreurs aux différentielles. Pour obtenir les incertitudes absolues, on majore les erreurs : cela revient à remplacer dans l'expression les différentielles par les incertitudes absolues. L'erreur étant a priori de signe inconnu, prendre le majorant conduit à passer aux valeurs absolues :
Ok, ça c'est compris, merci 
Après mon problème surtout, c'est que je suis perdu quand il faut calculer : ( U/
U/ X)
X) 
 X
X
Comment faut il faire ?
Donne un exemple de difficulté rencontrée. Sur le plan théorique général, il n'y a rien de plus à dire...
voilà mon exo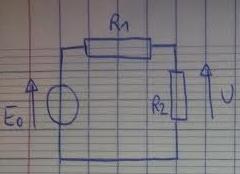
***Edit gbm : image recadrée, pour le texte, il faut l'écrire par tes propres soins sur le forum***
Voici le calcul... Revoie bien comment calculer une dérivée partielle.
Dans les cas simples de produits et/ou de quotient de grandeurs indépendantes, par exemple :
La méthode précédente permet de démontrer simplement que l'incertitude relative sur le résultat est la somme des incertitudes relatives sur les mesures :
Dans ton exercice, la difficulté vient du fait que R2 intervient à la fois au numérateur et au dénominateur de l'expression.


