Inscription / Connexion Nouveau Sujet
bougie conique
alors je n'arrive pas du tout a résoudre cet exo, j'ai meme vue une correction, mais je ne comprend toujours rien, voici l'enoncé:
Combustion d'une bougie de forme conique, ayant une base circulaire de rayon R, une hauteur totale H (et la pointe en haut).
1. En sachant que le volume de matière brûlée par unité de temps est constant dv/dt = Cste = C < 0, établir une équation différentielle pour l'évolution temporelle de la hauteur h(t) de la bougie. Aidez-vous en faisant un schéma.
2. À partir de l'équation différentielle trouvée, déterminer la valeur de la dérivée dh/dt de la solution h(t) pour t=(correspondant à h=H) et à l'instant final t=tf, lorsque h= 0
Pour la premiere question je comptais faire (dh(t)/dt)*(pi/3)*r^2= v(t) vu que la vitesse c'est la variation du volume de la bougie, mais je ne sais pas quoi faire pour obtenir une equa diff et on m'avais dit que mem ca c'est faux.
Merci en avance !
bonjour,
on te donne dV/dt = C <0
donc il faut évaluer dV qui dépend de h (cf dessin)
on considère un élément de volume infinitésimal en M (tel que OM=h), de hauteur dh
on sait calculer dV en fct de R, H, h et dh
puis on écrit la relation indiquée plus haut et on obtient une équa. diff.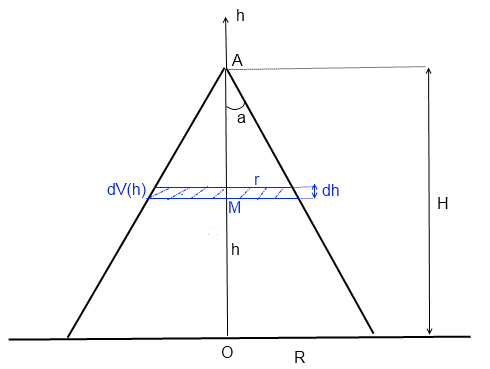
Edit Coll : image recadrée
alors je trouve dv= dh*(pi/3)*R^2
donc dv/dt= dh/dt*(pi/3)*R^2
donc dh/dt= 3C/pi*R^2
mais je n'obtient toujours pas une equation differentielle......


 dV
dV
 r2 dh
r2 dh

