Inscription / Connexion Nouveau Sujet
Barrage - Trop plein
Bonjour, je bataille sur un exercice depuis un bon moment déjà et je ne suis pas très sûr de moi...
Voici l'énoncé :
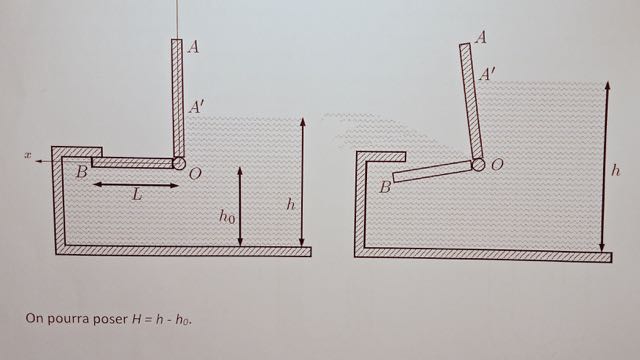
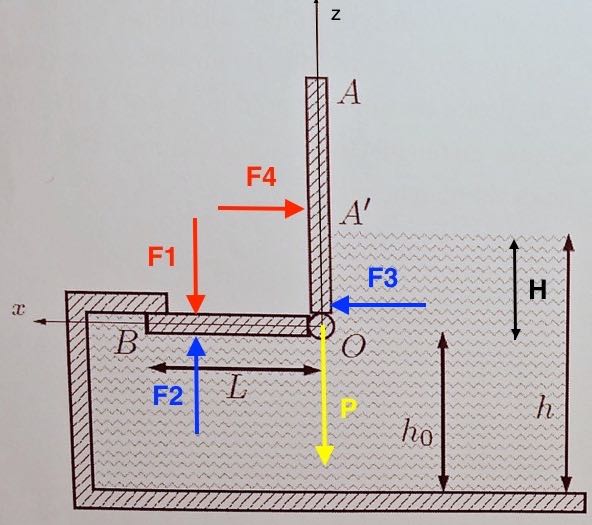
Une porte de trop-plein est représentée ci-dessous. Lorsque le niveau de l'eau h est trop haut, la porte AOB s'ouvre en tournant autour d'un axe perpendiculaire au dessin, passant par le point O, et laisse passer l'eau. On note A' le point de surface de l'eau. On négligera l'épaisseur de la porte.
1)Expliquer sommairement pourquoi la porte bascule lorsque la hauteur d'eau est trop élevée?
2)Enumérer et tracer sommairement les forces agissant sur la porte. On négligera ensuite le poids de la porte.
3)Calculer le moment en O des forces de pression exercées par l'eau et l'air sur la porte.
4)En négligeant le poids de la porte en déduire la hauteur h de liquide pour laquelle la porte bascule. Le résultat dépend-il de la pression atmosphérique?
J'ai joint le schéma de l'exercice.
Pour la première question, la porte bascule lorsque la hauteur d'eau est trop élevée car la pression de l'eau entre O et A' l'emporte sur l'équilibre de la porte.
Pour le seconde question, je suis moins sûr... il me semble qu'il y a 4 forces qui agissent sur la porte :
-le poids \vec{P} de la porte, dirigé vers le bas;
-la force de pression \vec{F} atm de l'ai sur la face horizontale de la porte, dirigée aussi vers le bas;
-la force de pression sur H, \vec{F} H horizontale et dirigée de droite à gauche,
-la force de pression de l'eau \vec{F} eau, dirigée vers le haut et s'appliquant sur la face horizontale de la porte.
Pour la troisième question, je tâtonne;
Le système est considéré à l'équilibre, donc \sum{W}\vec{F}est = \vec{0} mais je ne suis pas sûr de mes forces et j'ai un doute sur quel axe les projetter...
Si je choisi Ox, pour le force \vec{F} H c'est très bien, mais les autres sont nulles du coup...
Par contre pour la quatrième, je suis bloqué...
Vous pouvez m'aider?
Merci, bonne soirée.
Pour la 2, je te suggère de réfléchir sur ceci :
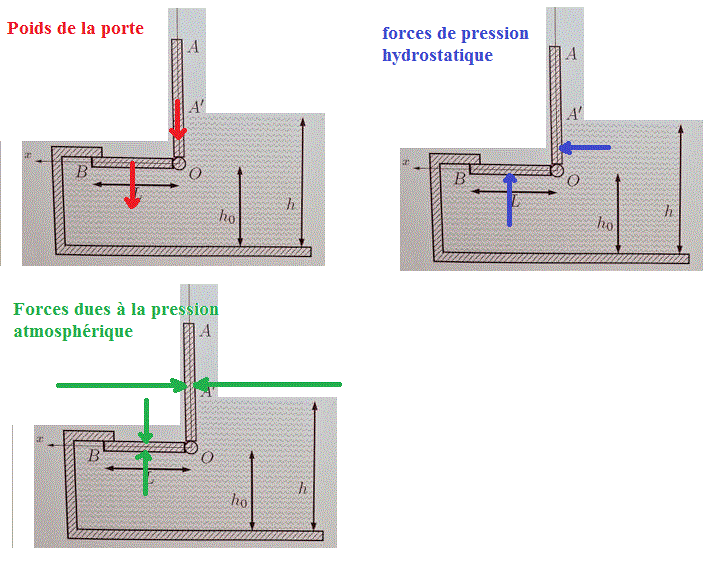
Ne pas se fier à l'échelle des forces d'un dessin à l'autre.

D'accord, c'est à peu près ce à quoi j'avais pensé.
Après, le poids de la porte est négligé, je ne l'ai pas fait apparaitre sur le dessin.
Si je fais le moment des forces :
Mais comment ensuite confronter les équation pour isoler H?
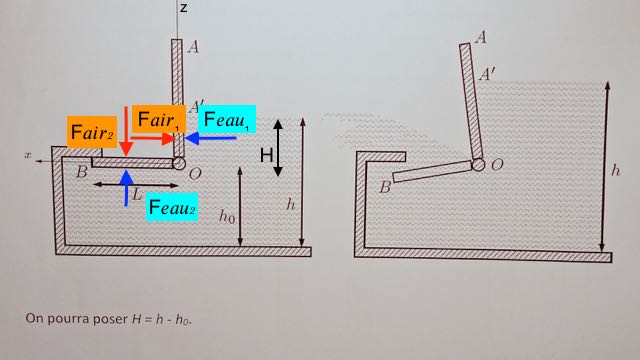
La pression atmosphérique ne joue aucun rôle.
En effet :
Sur la partie horizontale de la porte (OB) par exemple (en négligeant le poids comme précisé dans l'énoncé) :
La pression absolue sur le bas de la porte est P1 = Patmos + Rho(eau) * g * A'O
La pression absolue sur le haut de la porte est P2 = Patmos
Donc la force (verticale vers le haut) de pression sur la partie horizontale de la porte est : F = (P1 - P2) * S avec S la surface de cette partie de la porte (S = L * largeur)
F = (Patmos + Rho(eau) * g * A'O - Patmos) * L * largeur
F = (Rho(eau) * g * A'O) * L * largeur
... force indépendante de la pression atmosphérique, cette force est uniquement due à la pression due à la hauteur de la colonne d'eau.
Par un raisonnement analogue, la force résultante sur la partie verticale de la porte est démontrée aussi indépendante de la pression atmosphérique ... même pour la partie sous le niveau de l'eau.
Les amplitudes des forces est facile à trouver.
La seule petite difficulté de ce problème (pour calculer les moments) est de trouver l'emplacement du centre de poussée de la résultante de la force hydrostatique sur la parte verticale de la porte.
Sauf distraction.

D'accord, donc en reprenant le même raisonnement :
-pression de l'air sur la face gauche de la porte : P 𝑎𝑖r 1 = P 𝑎𝘵𝘮
-pression de l'eau sur la face droite de la porte : P 𝘦𝑎𝘶 1 = P 𝑎𝘵𝘮 + 𝜌.g.H (H=A'O)
Donc la force agissant sur la porte par la droite est :
= (P 𝘦𝑎𝘶 1 - P 𝑎𝑖r 1 )x (H.ℓ)
Ce qui donne : = 𝜌.g.H x (H.ℓ)
mais on ne connait pas la largeur de la porte non plus.
Donc, en synthétisant, il n'y a que deux forces de pression qui agissent sur les porte F1 et F2 (j'ai appelé F1, la première force que vous avez démontré.)
J'ai compris cependant que la pression de l'air n'intervenait pas.
Par contre pourquoi on demande de calculer le moment en O des forces de pression?
Je n'arrive pas à suivre le fil du problème...
"Par contre pourquoi on demande de calculer le moment en O des forces de pression? "
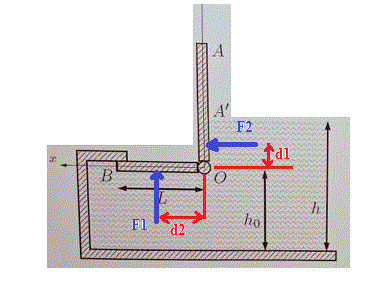
Le moment de la force F1 par rapport à l'axe passant par O est : M1 = - F1 * d1
Le moment de la force F2 par rapport à l'axe passant par O est : M2 = F2 * d2
Le moment résultant de toutes les forces appliquées à la porte par rapport à l'axe passant par O est M = M2 + M1
M = F2 * d2 - F1 * d1
La porte reste fermée si M < 0 (tente de pivoter autour de O dans le sens horlogique (anti trigonométrique))
La porte s'ouvre si M > 0 (tente de povoter autour de O dans le sens anti horlogique (trigonométrique))
La porte est donc à la "limite" de pivoter Pour M = 0
-----
Il faut donc trouver la hauteur h telle que M2 + M1 = 0, ce sera la hauteur h pour laquelle la porte est juste à la limite de basculer.
On peut soit calculer F1, F2, d1 et d2 et en déduire M1 et M1 et trouver h telle que F1*d1 = F2*d2
Ou bien on peut calculer M1 et M2 directement (sans passer par les calculs intermédiaires des forces et des distances) et ...
Le niveau de difficulté est sensiblement le même, il faut de toute manière passer par le calcul intégral.
-----
Remarques :
1) On n'a pas besoin de connaître la largeur de la porte ... du moins si on suppose qu'elle est partout la même.
Cette largeur va se supprimer dans les calculs et n'interviendra pas dans le résultat du calcul de h pour que la porte bascule.
2) Les forces résultantes (F1 et F2) sur les 2 morceaux de la porte (dans les conditions de l'énoncé) sont uniquement dues à la pression hydrostatique.
3) ATTENTION dans les calculs que la pression hydrostatique varie avec la profondeur, ce dont tu sembles bien ne pas tenir compte (par exemple dans ton calcul de F2).
Sauf distraction.

Bonjour,
Pour pourtant j'ai fait intervenir la hauteur H, ce n'est pas bon?
= 𝜌.g.H x (H.ℓ)
J'ai repris le problème depuis le début car je ne m'en sors pas...
Les forces appliquées à la porte :
-la force de pression
-la force de pression
-la force de pression
-la force de pression
-la pesanteur
En projetant sur l'axe des x, on a :
= ( P atm + 𝜌 eau . g . H).(H.ℓ)
= - P atm .(H.ℓ)
En projetant sur l'axes des y, on a :
= - P atm .(L.ℓ)
= P eau .(L.ℓ)
= m.g Le poids est négligé.
De là ensuite, on demande de calculer le moment des forces :
j'espère ne pas m'être trompé...
Mo() = F1.L
Mo( ) = - F2.L
Mo( ) = F3.H
Mo( ) = - F4.H
La porte est en équilibre donc si la somme des moments des forces est nul :
= 0
F1.L - F2.L + F3.H - F4.H = 0
( - P atm .(L.ℓ)) x L- P eau .(L.ℓ) x L + ( P atm + 𝜌 eau . g . H).(H.ℓ) x H - ( - P atm .(H.ℓ) ) x H = 0
- P atm .(L².ℓ) - P eau .(L².ℓ) + P atm .(H².ℓ) + 𝜌 eau . g . H³.ℓ) + P atm .(H².ℓ) = 0
Je m'enfonce dans un calcul sans issue....
En suivant ce cheminement, comment faire disparaitre la pression atmosphérique? Je comprend le raisonnement que vous avez tenu au-dessus pour éliminer la pression atmosphérique puis le principe d'équilibre pour déterminer H mais après...
Vous dites qu'il faut utiliser le calcul intégral, je vois tout à fait en Mathématiques ce que c'est mais je n'ai pas abordé encore ces notions en physique. Les leçons que j'ai couvertes pour ces exercices n'en parlent pas encore. Je vais continuer à batailler.
Joyeux Noel dans tous les cas et merci beaucoup!
Je ne passe pas mon temps à calculer avec la pression atmosphérique ... puisque son effet est nul dans le cas présent.
Je prends mes notations (dessin du 25-12-16 à 10:41)
pression hydrostatique au niveau BO : P1 = Rho*g * (h-ho)
F1 = P1 * L * largeur
F1 = Rho*g * (h-ho) * L * largeur
Moment de F1 autour de l'axe O : M1 = - F1 * L/2
M1 = - Rho*g * (h-ho) * L² * largeur/2
-----
On peut calculer M2 sans passer par le calcul de F2, par exemple ainsi :
En notant z la profondeur (sous le niveau de A') :
La pression à la profondeur z est : P(z) = Rho.g.z
La distance entre la profodeur z et le point O est : (h - ho) - z
-----
Le moment résultant de toutes les forces appliquées à la porte autour de l'axe passant par est M = M1 + M2
M = Rho.g.Largeur . (h - ho)^3/6 - Rho*g * (h-ho) * L² * largeur/2
La valeur de h telle que la porte est à la limite de basculement est celle pour laquelle M = 0
--> pour : Rho.g.Largeur . (h - ho)^3/6 = Rho*g * (h-ho) * L² * largeur/2
(h - ho)^3/6 = (h-ho) * L² /2
(h - ho)^2/3 = L²
(h-ho)² = 3L²
-----
Sauf distraction. (rien relu) 
Hello JP
La pression atmosphérique ne joue aucun rôle
Pas tout à fait il me semble ...
Sur la porte horizontale la variation de la contribution des pressions atmosphériques dans les forces des pressions F1 et F2 est
 P =
P =  air.g.A'O
air.g.A'O
On choisira peut être négliger de négliger ce rôle
Sauf négligence coupable de ma part?

Salut dirac,
Oui, pour moi, on néglige.
C'est en tout cas absolument dans l'ordre des choses ...
Et surtout en ayant déjà négligé par énoncé des "choses" bien plus importantes, comme le poids de la porte et son épaisseur.
Remarque que d'autres phénomènes ont été (à juste titre encore) négligés ... comme par exemple la variation de la masse volumique de l'eau avec la profondeur (donc la pression) car l'eau n'est que "quasi" incompressible.
Juste pour info :
Ici : ![]() , il y a un calculateur de la masse volumique de l'eau en fonction de la température et de la pression.
, il y a un calculateur de la masse volumique de l'eau en fonction de la température et de la pression.
On a par exemple : à T = 10°C
A 0 bar: 999,7 kg/m³
A 1 bars : 999,75 kg/m³
A 10 bars : 1000,18 kg/m³
A 100 bars : 104,43 kg/m³
On peut aussi noter la variation de g avec l'altitude et plein d'autre choses ... dont les influences sur le résultat sont peanuts sur le résultat.

Hello JP
Mon commentaire se voulait un clin d'oeil (très amical) sur le thème "mais sait on en fait pourquoi on fait certaines hypothèses et pourquoi on néglige certaines chose" (en référence à un précédent msg un peu sur le même thème). A me relire le côté "clin d'oeil amical" ne ressortait pas il est vrai.
Avec toute ma considération (et mes remerciements pour tes relectures vigilantes ...) 
Bonjour,
Dans l'énoncé, on me demande justement de calculer les moments des forces de pression exercées par l'air et l'eau sur la porte, c'est pour cela que j'essaye de les calculer.
La force de pression de l'air est peut être négligeable ou bien elle s'élimine dans le calcul, je ne sais pas. Le fait est que je ne peux conclure que la pression atmosphérique n'intervient pas qu'à la dernière question.
Par ailleurs, pourquoi divisez-vous la largeur L par deux? Et pourquoi n'utilisez-vous le calcul intégral que pour M2?
J'ai trouvé un peu de documentation qui devrait m'aider à résoudre ce problème sur cette page (notamment au paragraphe 3) :
http://bts-sciencesphysiques.org/cours/mecanique_fluides/hydrostatique.pdf
Merci encore. Bien cordialement.
Hors topic,
"mais sait on en fait pourquoi on fait certaines hypothèses et pourquoi on néglige certaines chose"
Pourquoi on néglige certaines choses ?
Parce qu'il est impossible de tenir compte de "tout".
Un exemple simple (mais que l'aime bien)
Si on veut déterminer l'emplacement du point d'impact d'un caillou laché du haut de la tour Eiffel.
Si on considère un référentiel terrestre comme galiléen pour ce faire ... on fait des erreurs.
- On néglige ainsi, entre-autres, le fait que la Terre tourne autour de son axe polaire. (et donc l'effet Coriolis)
Si on veut éviter cette erreur, soit on conserve le même référentiel et on introduit la correction voulue pour tenir compte de l'effet Coriolis ... ou bien on utilise un référentiel géocentrique.
Mais ceci entraîne des calculs plus dificiles.
Oui mais, que penser de la position de la lune quand on fait l'étude ?
il y a bien une force de gravitation caillou-lune pendant la chute et donc un effet sur la position du point d'impact.
Et que penser du vent ? surtout si il souffle par bourrasques ?
Et quid du fait que même si on utilise un référentiel géocentrique, il n'est quand même pas parfaitement galiléen et que donc cela entraînera aussi des erreurs...
Donc prenons un référentiel héliocentrique, c'est déjà moins "mal galiléen". Certes, mais les calculs de la chute du caillou sont maintenant plus que compliqués ...
et il subsistera encore des erreurs (car ce référentiel n'est pas parfaitement galiléen non plus), donc prenons ...
Bref, il est impossible de tenir compte de tout et à chaque pas qu'on fait pour minimiser les erreurs, les calculs se complexifient très vie de manière abominable.
On est donc bien obligé de "négliger" certaines choses pour pouvoir réaliser une étude.
Encore faut-il pouvoir estimer l'ordre de grandeur des effets des "choses" négligées pour voir si le résultat sera acceptable avec la précision dont on a besoin dans l'exploitation de la réponse qu'on trouvera du problème.
... Et c'est là qu'est l'os pour beaucoup.
Par exemple négliger ici l'effet Coriolis entraîne une erreur de l'ordre de 8 cm sur la position du point d'impact. (le "sentir" sans calculs n'est pas à la portée de tous)
Si le but est de tomber à l'intérieur d'une cible de 5 m de diamètre ... no problem.
Mais si on désire toucher une cible de la taille d'une pièce de 2 euros ...
Quant à la position de la lune, qui peut estimer sans calculs (grossiers) de son effet sur la position du point d'impact.
...
Bref, dans le secondaire, aucun (ou alors qu'il me fasse signe) étudiant n'est capable de "juger" par lui même si il peut au non négliger certains effets, c'est le prof qui lui dit (et pas sûr du tout d'ailleurs que la plupart des profs soit capables d'estimer ces erreurs)
Donc, impossible de "tenir compte" de tout et obligation de négliger une multitude d'effets ... Mais en étant capable d'estimer l'ordre de grandeur des erreurs faites en négligeant ces effets pour juger si les résultats de l'étude "simplifiée" sont acceptables avec la précision dont on a besoin.

Laurent,
Par ailleurs, pourquoi divisez-vous la largeur L par deux? Et pourquoi n'utilisez-vous le calcul intégral que pour M2?
Dans le cas de la partie horizontale de la porte :
La force de pression résultante est facile à calculer sans intégrale (puisque cette partie de porte est entièrement à la même profondeur) et le point d'application de cette force est "évident (pour raison de symétrie), il est au milieu de la porte (d'où le L/2 en calculant le moment)
On pourrait parfaitement utiliser le calcul intégral et trouver la même chose.
Pour la partie verticale de la porte :
C'est moins intuitif, en effet, la pression hydrostatique augmente avec la profondeur et il est donc évident que le point d'application de la résultante des forces de pression sur cette partie de la porte n'est pas au milieu de la partie immergée.
Pour calculer la force résultante, c'est facile à calculer sans intégrale (et pourtant ton calcul était faux)
Par contre pour trouver l'emplacement du point d'application (en tenant compte que le pression varie avec la profondeur), il faut passer par un calcul intégral (simple).
Et on peut aussi calculer directement le moment (sans calculer séparément F et le bras de levier), mais il faut aussi passer par un calcul intégral (celui que j'ai fait).



