Inscription / Connexion Nouveau Sujet
Automatique : fonction de transfert
Bonjour,
J'ai quelques incompréhensions dans mon cours d'automatique.
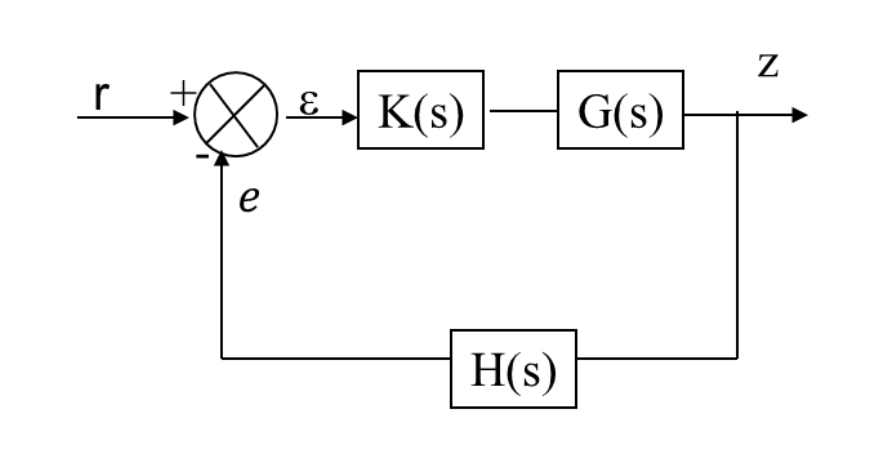
La fonction de transfert en régime ouvert est définie par (fig 1): . Je ne comprends pas. J'aurais remplacer e par z dans cette formule.
En boucle fermée, elle est définie par : . Pourquoi z dans ce cas ?
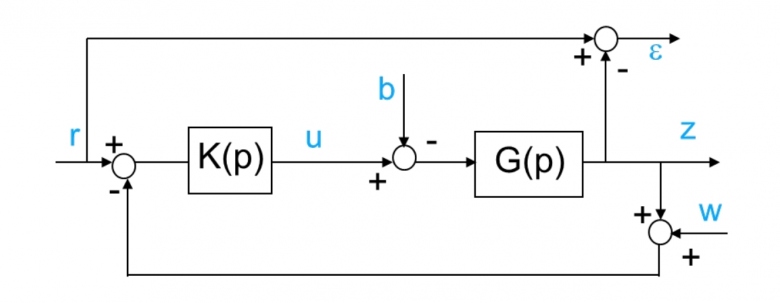
Je n'arrive pas à retrouver les résultats de la figure 2. Par exemple la fonction de transfert de vers
est donnée par
.
Enfin, je ne semble pas avoir bien compris les principes de l'automatique. Par exemple, comment délimiter le système ? Comment le définir ? Je pense que c'est l'objet qui contient la grandeur à asservir mais pas sûr.
Merci d'avance pour les réponses.
Bonsoir,
Pour ce soir, je poste uniquement un pdf dont le début répondra peut-être à tes interrogations. Tu auras surement d'autres réponses, sinon à demain pour la suite.
PDF - 424 Ko
Bonjour,
Pour ce qui est de la boucle ouverte (GBO), il vaut mieux prendre le problème à l'envers : toutes les études (en particulier le gain en boucle fermé) font intervenir et donc KGH (et sa position par rapport à -1). On a donc donné un nom à ce KGH : GBO. Après on peut essayer de justifier le nom : il y a un cas simple dans lequel il est parfaitement justifié : le retour unitaire (H=1), dans ce cas GBO=z/r=sortie/entrée (comme vous le pensiez) lorsqu'on ne fait pas de retour sur la borne moins (boucle ouverte). Le fait de prendre e comme sortie est là pour retomber sur KGH.
Les calculs reposent essentiellement sur la traduction du schéma. Pour votre exemple, on veut une relation entre ε et r : on part du soustracteur ε=r-e, et on se débarrasse de e en remontant dans le schéma jusqu'à ε : e=KGH ε. Ce qui donne ε(1+KGH)=r.
Le système dépend du contexte, de l'étude que vous faites ...
Dans votre schéma de principe, le système initial/brut c'est G, H c'est le capteur, K est la commande/correcteur. Et le système global/asservi c'est le tout : entrée r, sortie z.
Bonjour,
Petits compléments...
Pour la figure 1, comme on est en régime ouvert, e n'est déconnecté du comparateur ce qui entraîne en particulier que 
=r. Mais comme l'auteur demande e/, c'est simplement le produit des blocs entre l'entrée et la "sortie" e donc K*G*H.
Pour la figure 2, on ne s'intéresse qu'à la réponse à r, donc on fait comme si b et w n'existaient pas. Pour l'étude complète, on utiliserait le théorème de superposition en étudiant successivement les réponses à r, b et w.
Donc, pour /r, on a
=r-z relation(1)
z=G*K*(r-z) relation (2)
d'où par élimination de z entre (1) et (2), je n'obtiens pas exactement la relation donnée. Qu'en pense gts2 ?
Bonjour,
J'avais en effet traité le premier schéma.
Pour celui en dessous, on lit :
(1) ε=r-z (soustracteur du haut)
(2) z=(r-z)KG (ligne du milieu, la sortie du soustracteur du bas (entrée de K) est r-z lorsque w=0)
soit z=εKG qui reporté dans (1) donne
ε(1+KG)=r
Annuler
connectez vous