Bonjour
Il suffit d'appliquer les relation valides pour un mouvement rectiligne d'accélération constante en choisissant convenablement les conditions initiales et le repère.

Rappel des "formules" dans mon message du  29-03-20 à 17:25 ici :
Cinématique"

S'agit-il d'un exercice demandé par ton professeur ou d'un exercice dont tu as "inventé" l'énoncé ?
Tu peux clairement modéliser le parcours au sol par un mouvement uniformément retardé. Il faudrait alors trouver l'abscisse x3 du contact avec le sol et la vitesse v3 correspondante.
En revanche, il faut faire des hypothèse sur le mouvement d'approche dans l'air. Passer de l'altitude de 10000m à l'altitude nulle pour une variation d'abscisse inférieure à 700m : cela représente une descente presque verticale : totalement invraisemblable pour un avion de ligne et totalement incompatible avec un angle d'approche de 40°.
Si tu définit cet angle d'approche comme l'angle entre la trajectoire de l'avion supposée rectiligne et l'horizontale, l'angle d'approche doit être beaucoup plus faible pour éviter un atterrissage brutal. Il est en général de l'ordre de 3°. Cela suppose, pour un atterrissage en x3=600m, une valeur de yo d'environ 30m. Nous sommes loin des 10000m que tu proposes !
Si tu pouvais reformuler tout cela et faire un schéma que tu pourrais scanner et poster ici...

Voici un schema pour illustrer.
Nous connaissons H, Vix, Viy, Vfy, x1 , x2 , L et l'angle d'approche.

Pourquoi ne pas choisir x=0 à l'instant correspondant au début de l'approche ? Ainsi :
x_o=0 ; y_o=H ?
Le point A correspondant à la position où l'avion se pose a dans ces conditions une abscisse x₃ telle que :


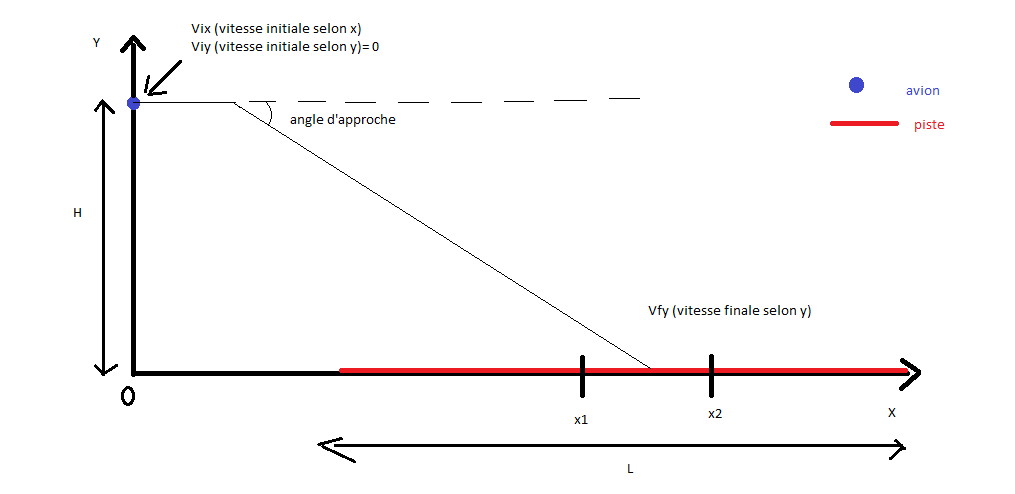
où est l'angle d'approche. Quelles sont les questions exactement ?