Inscription / Connexion Nouveau Sujet
Aspirateur
Bonjour,
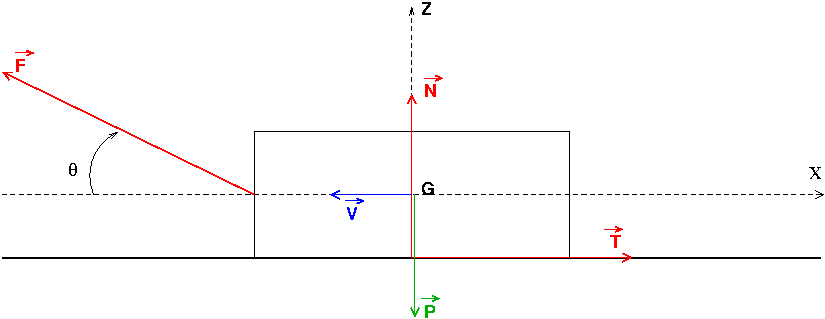
un ustensile ménager est constitué d'un bloc solide de masse M qui glisse sur le sol avec un coefficient de frottement  . Une tige de masse négligeable, articulée idéalement au niveau du bloc, permet de tirer ou pousser celui-ci : l'opérateur exerce une force F en fonction de l'angle
. Une tige de masse négligeable, articulée idéalement au niveau du bloc, permet de tirer ou pousser celui-ci : l'opérateur exerce une force F en fonction de l'angle  entre la tige et le sol, lorsque le bloc est en translation rectiligne uniforme sur le sol.
entre la tige et le sol, lorsque le bloc est en translation rectiligne uniforme sur le sol.
Exprimer F( ) lorsque l'on tire l'ustensile.
) lorsque l'on tire l'ustensile.
Je pense pouvoir réussir l'exercice seul, mais mon schéma de base doit être faux, pourriez vous me donner une représentation de la situation, axes etc... svp
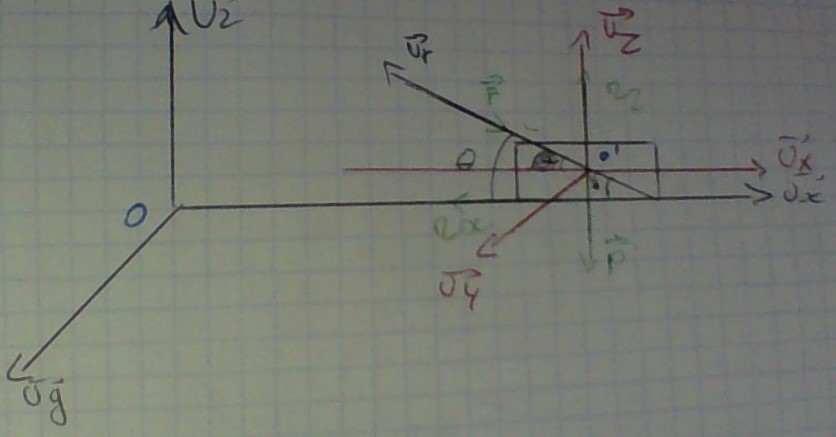
OK pour T et F sauf que si tu tires l'objet vers la gauche, F a le sens de Ur; pour la réaction du sol : tu la décompose en 2 : une réaction normale de vecteur N verticale ascendante ; une composante horizontale T orienté dans le sens opposé à celui du mouvement(force de frottement solide).
Tu te places j'imagine dans l'approximation quasi statique : l'accélération est suffisamment faible pour que les lois de la statique puissent s'appliquer en bonne approximation. Dans ces conditions, tu écris que la résultante des vecteur forces est le vecteur nul. Tu projettes sur les axes Ux et Uz et tu tiens compte des lois de Coulomb sur les frottements
Je comprend mieux pourquoi je n'y arrivais pas, je voulais m'avancer dans une feuille d'exercice mais je n'ai pas encore vu la loi de Coulombs, pourriez vous s'il vous plaît me l'expliquer brièvement ?
Dans le cas simple d'un glissement, la réaction tangentielle à la direction et le sens du vecteur où
désigne le vecteur vitesse de glissement du solide par rapport au sol et sa norme vaut :T = µ.N où µ désigne le coefficient de frottement dynamique (souvent noté f plutôt que µ). Dans ton problème, il suffit d'orienter le vecteur T suivant Ux si le mouvement de glissement se fait vers la gauche.
Remarque : il faut considérer dans ton problème le solide de longueur faible, sinon, le fait que la force de traction s'exerce à l'avant du solide rend la pression exercée par le solide sur le sol plus importante à l'arrière du solide qu'à l'avant. Dans ce cas, l'application des lois de Coulomb est plus compliquée mais je ne pense pas que cela te soit demandé.
Voici le schéma( en fait quasiment le tien..)
Je traite l'exemple où le solide est tiré vers la gauche. Je te laisse traiter le cas du solide poussé vers la droite.