Bonjour
De façon générale, si H=A+jB
=Arg(H) vérifie :
tan()=B/A avec cos() du signe de A et sin() du signe de B.
Dans ton exemple : tan()=-L/R avec cos()<0 et sin()>0 ; reprends un cercle trigonométrique si cela ne te parait pas cohérent : ]/2 , [ modulo 2rad bien sûr.
Revois maintenant les propriétés de la fonction arctangente (ici par exemple : ) Pour obtenir une fonction bijective, le domaine des valeurs possibles de est limité à l'intervalle ]-/2 , /2[ c'est à dire limité aux domaines tel que cos()>0.
Conséquence : si H=A+jB, écrire =arctan(B/A) n'est possible que si A>0.
Si A est négatif comme ici : petite astuce :
H=(-1).(R-jL). L'argument d'un produit étant la somme des arguments des différents termes du produit :
=arg(-1)+arg(R-jL)=+arctan(-L/R) (modulo 2 rad bien sûr).

Bonjour fm_31
Il me semble bien que la fonction arctangente est impaire :
arctan(-x)=-arctan(x)
mais tu as raison : autant simplifier...

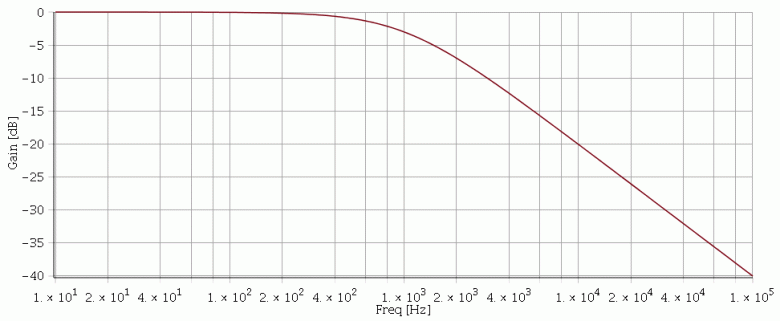
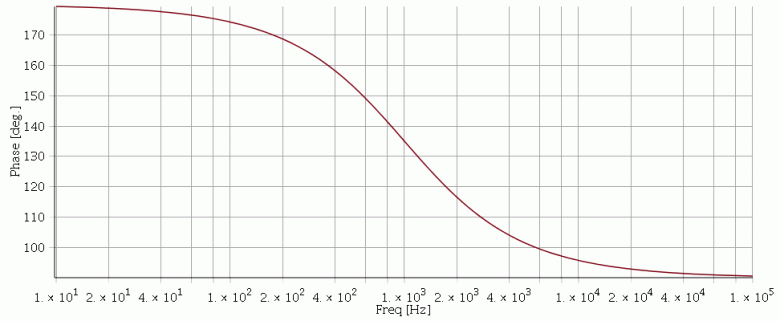
Pour illustrer mon propos précédent, je prends l'exemple d'un filtre passe bas inverseur du premier ordre :







Le diagramme de Bode est tracé pour une fréquence de coupure de 1kHz.

Ok merci beaucoup c'est plus clair maintenant
Pour résumer, si je ne me trompe pas, à chaque fois qu'on a A<0 dans la "formule complexe" ou un réel inférieur à 0 on rajoute pour passer à Arctan ?

Pour être sure de ne pas te tromper dans les signes, utilise l'astuce que je t'ai indiquée consistant à multiplier par  (-1) tout en inversant les signes du complexe pour obtenir un complexe de partie réelle positive.

Ok d'accord je ferai ça merci beaucoup