Inscription / Connexion Nouveau Sujet
Approche énergétique
Bonjour, je suis nouveau sur ce forum alors je me présente ! Je m'appelle Frédéric, je suis étudiant en première année d'école d'ingénieur et je viens à vous pour fignoler un exercice, surement pas bien difficile, mais qui me casse la tête...
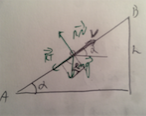
C'est l'histoire d'une petite bille, qui veut se déplacer de A à B avec un coefficient de frottement f, ci joint le schéma du problème. Il faut déterminer la vitesse minimale qu'il faut communiquer à la bille en A pour qu'elle atteigne B.
Dans un premier temps, j'ai calculé les différents travaux qui s'appliquent:
, car RN est orthogonale à dOM
Je commence à être embêter ...
Je dis que
Or, d'après Coulon,
donc,
De là je projete le PFD sur les axes (RN,V)
, or a est nul ici donc
Dans W(RT),
De la, je suis perdu.. je pense meme mettre tromper au travail de RT !
Mais je pensais écrire que EC=EPp+E(RT)
donc
et de la j'extrais v, mais je pense que ça ne va pas!
Donc voila, j'ai grandement besoin de votre aide! je suis perdu....
D'avance, merci !
Bonsoir
Assez bien vu mais tout de même une erreur... Je ne comprends pas ton "carré".
Loi de Coulomb : ; en reportant dans l'équation ci-dessus :
Théorème de l'énergie cinétique : ; après simplification :
J'ai quasiment tout compris !!! Je te remercie !! Juste, pourrais tu détailler le travail de RT? D'ou vient la distance AB?
Je me réponds ! Revenir à la définition... W(F)=F*Distance*cos(alpha)....
Je te remercie grandement, bonne soirée  !
!
Attention, on ne raisonne pas à coup de formules retenues par coeur sans en comprendre la portée.
Tu ajoutes des sin et des cos un peu au petit bonheur la chance
L'énergie cinétique d'un mobile de masse m animé d'une vitesse v est : Ec = 1/2 m.v²
Les directions et sens de la vitesse n'ont rien à y voir.
Donc, que fait le sin(alpha) dans le 1/2 m v² . sin(alpha) dans ton message initial ?
-----
La travail du poids de la masse m entre A et B est : W1 = m.g.(altitude de A - altitude de B)
Or (altitude de A - altitude de B) = - AB.sin(alpha) (simple application trigonométrique dans le triangle ABC (avec C la projection orthogonale de B sur l'horizontale passant par A)
Et donc W1 = -mg.AB.sin(alpha)
Habituellement, on nomme h la différence d'altitude entre A et B ... et donc ton mgh.sin(alpha) est faux.... car la distance AB n'a évidemment la même valeur que AC (avec C défini ici plus avant)
-----
Quant à ton terme : f.(m*g.cos(alpha))² il ne peut être que faux, ne serait-ce que parce qu'il n'a pas la dimension d'une énergie (Travail) comme les autres termes de l'équation.
La force de frottement est proportionnelle à la composante normale de la réaction du support sur la masse m.
La composante normale de la réaction du support est N = mg*cos(alpha) (qui se trouve facilement en tenant compte que l'objet ne s'enfonce pas dans le support et n'en décolle pas non plus)
Donc la force de frottement est égale à FF = f*N = f*mg.cos(alpha) (avec f le coefficient de frottement), cette force a même direction que le déplacement mais est de sens contraire
Le travail W2 de la force de frottement sur la distance AB est donc W2 = - FF * AB = - f*mg.cos(alpha) * AB
Ce qui n'a vraiment rien à voir avec ton -f*(cos(alpha)*m*g)² ... outre les erreurs de dimensions, on ne voit nulle part la dedans en quoi la distance parcourue (AB) pourrait intervenir ... et pourtant elle doit intervenir.
-----
On devrait donc avoir :
1/2.m.Vo² + W1 + W2 = 0 (puisque le mobile arrive en B à vitesse nulle)
1/2.m.Vo² -mg.AB.sin(alpha) - f*mg.cos(alpha) * AB = 0
Vo² = 2.(g.AB.sin(alpha) + f*g.cos(alpha) * AB)
Vo² = 2.g.AB.(sin(alpha) + f*cos(alpha))
Si on préfère exprimer Vo en fonction de H (différence d'altitude entre A et B) au lieu de la distance AB, on introduit H = AB.sin(alpha) dans la relation ci dessus ...
Et on arrive alors à l'expression donnée par vanoise.
Peu importe la relation finale utilisée, elles sont équivalentes.
MAIS il est impératif de comprendre le pourquoi de chaque étape du raisonnement et pas faire un raisonnement en se cachant derrière des formules dont on ne maîtrise pas la portée... et qui entraînent forcément des erreurs.



