Inscription / Connexion Nouveau Sujet
Appliquer Millman pour un AOP
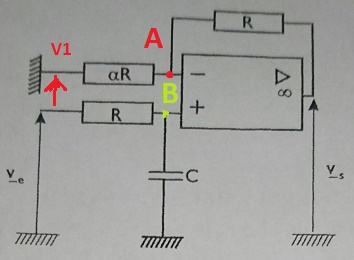
Bonsoir,j'essai d'utiliser Millman(uniquement si possible) pour trouver vs/ve pour le schéma ci-dessous.
Je sais que c'est la loi des nœuds appliqué aux potentiel,mais j'essaie de bien comprendre la méthode et de l'appliqué.
Pour l'instant voici ce que j'ai pu dire:
d'ou .
Donc
Mais j'ignore ce que vaut le V1 ,cependant je pense que mon Va,V- et V+ sont bon,après pour trouvé vs/ve c'est là que ça coince.
Bonsoir
Plusieurs confusions ou erreurs :
1° : L'entrée inverseuse, souvent notée E-, est celle que tu notes A sur ton schéma ; l'entrée non inverseuse, souvent notée E+, est celle que tu notes B. Pourquoi, dans ces conditions, faire la distinction entre VA et V- et la distinction entre V+ et VB ?
2° : Le fait que l'A.O. soit considéré comme parfait et fonctionne en régime linéaire impose V+ = V- (soit ici VA = VB) mais la valeur commune n'est pas nécessairement nulle si aucune de ces deux entrées n'est reliée à la masse.
2° : As-tu bien compris ce que représente une masse sur un schéma ? C'est un nœud dont le potentiel est nul. Le potentiel de la borne "de gauche" de la résistance  R est donc nul. Que vient faire la tension V1 ici ?
R est donc nul. Que vient faire la tension V1 ici ?
Essaie de reprendre ton raisonnement en tenant compte de ces remarques...
La méthode consiste à appliquer le théorème de Millman aux nœuds A et B puis à écrire VA=VB.
Oui,voila je voulais nommé correctement ces tensions!
Ok,donc on a :
.
Puis on a:
Ensuite comme l''AOP est idéal(énoncé) on a V+=V- ce qui permet normalement de trouvé Vs/Ve vu qu'on a Vs et Ve dans les 2 expressions.
Bonjour
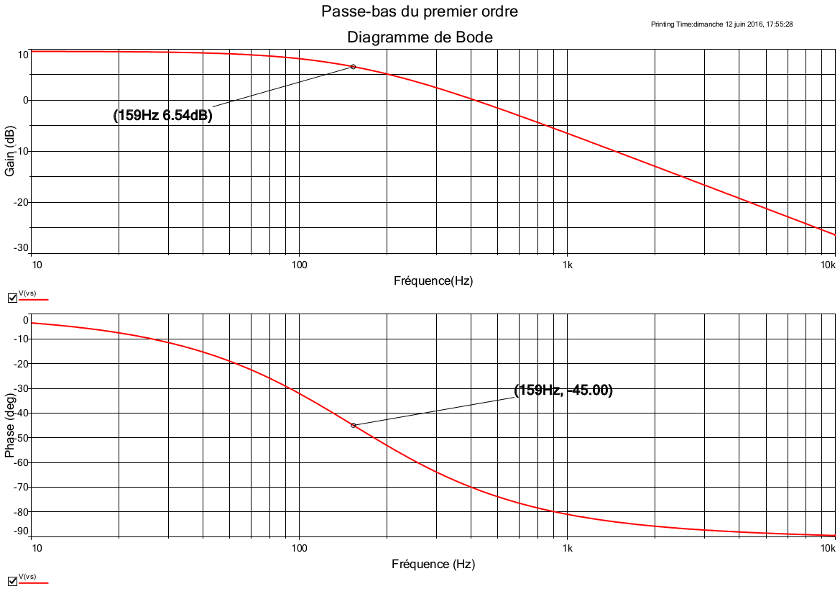
Voilà qui est beaucoup mieux ! Tu devrais obtenir un passe-bas du premier ordre avec :
et :
Voici le diagramme de Bode pour  =0,5 et
=0,5 et  o=1000rad/s.
o=1000rad/s.