Inscription / Connexion Nouveau Sujet
application théorème de Gauss
Bonsoir,
j'ai un exercice où je dois appliquer le théorème de Gauss pour déterminer un champ électrique et je suis un peu confus pour appliquer réellement le théorème au delà de l'aspect théorique. Je vois plusieurs méthodes et je ne sais pas laquelle utiliser...
on a la situation d'un orage :
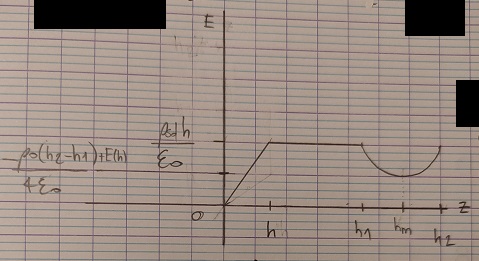
++++++++++++++++++++++++++ h2
------------------------------------------- h1
++++++++++++++++++++++++++ h
_______________________________________0 (sol)
Avec l'axe (Oz) dirigé vers le haut de vecteur unitaire .
Je sais que le champ electrique est de la forme
Je dois calculer le champ électrique entre "h" et "h1".
Première méthode
ensuite à gauche on "sort" E(z) de l'intégrale (car constant sur la surface qu'on a choisi, mais avec cette méthode on a pas besoin de spécifier précisément la surface je crois ?) et on a :
et donc
est la réponse.
Est-ce que c'est une bonne méthode ? Le résultat est-il bon ? Je trouve cette méthode un peu moyenne car à mon avis ce n'est pas très rigoureux ce qu'on fait avec les triples intégrales pour les passer en simples intégrales... mais je ne sais pas ça se trouve c'est très bien.
L'autre méthode : on définit la surface de Gauss comme étant un cylindre avec la base (surface D1) du cylindre au niveau de "h", et le sommet (surface D2) au niveau de "h1". Le flux au niveau de la surface latérale est nul donc on a :
Je ne trouve pas le même résultat... j'ai lu plusieurs ressources sur internet mais je ne vois pas comment ces deux méthodes peuvent donner le même résultat, la deuxième paraît aussi beaucoup plus compliquée :/
Quelle est mon erreur ? Quelle méthode est mieux en général ?
Merci d'avance pour votre aide
Bonsoir
Utiliser le théorème de Gauss est simple seulement si la source du champ possède suffisamment de symétrie et dinvariances. Peux-tu fournir un énoncé complet du problème ainsi qu'un scan du schéma qui l'accompagne ?
Bonsoir,
Oui, voilà le schéma en pièce-jointe.
L'énoncé est :
On considère un nuage situé entre les altitudes h1 = 2 km et h2 = 10 km. On suppose qu'on étudie les phénomènes loin des bords du nuage. On peut donc considérer qu'il n'y a pas d'effets de bord et que toutes les grandeurs sont fonction seulement de l'altitude z. La base du nuage est chargée négativement et charge positivement par influence une couche d'air au voisinage du sol, comprise entre les altitudes 0 et h = 500 m.
1. Montrer qu'en tout point M de l'espace, le champ électrique peut se mettre sous la forme :
2. On suppose que ces charges sont réparties uniformément en volume avec une densité ρsolentre les altitudes 0 et h. Calculer E(z) dans cette zone. On supposera que le champ est nul en z = 0 et on appliquera le théorème de Gauss sur un cylindre vertical.
3. On a pu mesurer E(h) = 54 kV m-1. En déduire l'ordre de grandeur de ρsol et de la charge totale qui se trouve près du sol sous le nuage, Qsol. On suppose que le nuage a une section S = 1 km2.
4. Calculer le champ électrique dans la zone h < z < h1.
5.On suppose que le nuage est chargé négativement à sa base et positivement au sommet avec une variation linéaire entre ρ(h1) = -ρ0 et ρ(h2) = +ρ0. Donnez l'expression de ρ(z) à l'intérieur du nuage.
6.En utilisant le théorème de Gauss, montrer que le champ électrique à l'intérieur du nuage s'écrit :
en introduisant
Il a + de questions après... mais ma question porte sur la question 4)
Surface de Gauss : cylindre d'axe vertical dont la base d'aire S est en z=0 et la base supérieure à l'altitude z .
Surface de Gauss : cylindre d'axe vertical dont la base d'aire S est en z=0 et la base supérieure à l'altitude z .
Mais pour la question 4 pour calculer le champ entre h et h1 le cylindre doit avoir sa base en "h" et non en 0, ou je me trompe ? Et concernant la première méthode "sans cylindre", elle est valide et je peux l'appliquer ici ou pas ?
car constant sur la surface qu'on a choisi, mais avec cette méthode on a pas besoin de spécifier précisément la surface je crois ?
C'est là que tu te trompes !
Avant d'utiliser le théorème de Gauss, il faut soigneusement étudier les symétries et les invariances. C'est cela qui conduit à
1° : flux nul à travers le disque de base en z= 0 puisque
2° : expression très simple du flux à travers le disque en z>0 puisque
3° : flux nul à travers la surface latérale du cylindre puisqu'en tout point de celle-ci :
car constant sur la surface qu'on a choisi, mais avec cette méthode on a pas besoin de spécifier précisément la surface je crois ?
C'est là que tu te trompes !
Avant d'utiliser le théorème de Gauss, il faut soigneusement étudier les symétries et les invariances. C'est cela qui conduit à
1° : flux nul à travers le disque de base en z= 0 puisque
2° : expression très simple du flux à travers le disque en z>0 puisque
3° : flux nul à travers la surface latérale du cylindre puisqu'en tout point de celle-ci :
D'accord merci pour ces précisions, donc je dois forcément utiliser la seconde méthode avec le cylindre et considérer les deux disques. Si le disque de base est en 0, le flux sera nul et je pourrais l'enlever de l'équation.
Cependant j'ai toujours une interrogation car la question 4) dit de calculer le champ entre "h1" et "h" or si le cylindre commence en 0 (plus bas que h) on va calculer le champ entre "0" et "h1"... je ne vois pas comment est-ce qu'on calcule le champ électrique entre "h1" et "h" avec un cylindre avec sa base sur z=0 désolé

Question 2 : il te faut établir l'expression de Ez(z) pour 0<z<h. Pour cela, tu choisis un cylindre comme surface de Gauss dont les disques de bases sont en z= 0 et en z compris entre zéro et h. Tu calcules la charge électrique à l'intérieur de ce cylindre puis appliques le théorème de Gauss.
vanoise
Question 2 : il te faut établir l'expression de Ez(z) pour 0<z<h. Pour cela, tu choisis un cylindre comme surface de Gauss dont les disques de bases sont en z= 0 et en z compris entre zéro et h. Tu calcules la charge électrique à l'intérieur de ce cylindre puis appliques le théorème de Gauss.
Donc si j'applique le théorème de Gauss, en considérant que le flux du champ électrique à travers la surface latérale est nulle j'ai :
Comme le champ en z=0 est nul on a :
Concernant la question 3 je trouve :
Et pour la 4), en appliquant le théorème de Gauss avec un cylindre entre h et h1, étant donné qu'on a aucune charge entre h et h1 , on a :
Et donc le champ électrique reste constant entre h et h1. C'est bon jusque là ? (J'ai réussi la 5 aussi mais la 6 je bloque sur la forme à trouver).
Bonjour ferality et Vanoise,
Pour la 4) le résultat me paraît juste mais je dirais plutôt :
"Pour h<z< h1 on applique le théorème de Gauss entre 0 et z "
"Pour h<z< h1 on applique le théorème de Gauss entre 0 et z "
Entre O et z ou entre h et z : les deux méthodes se valent et conduisent au même résultat. Question de "feeling" !

Pour 6 : on écrit
 =A.z+B et on trouve les constantes A et B à partir des valeurs de
=A.z+B et on trouve les constantes A et B à partir des valeurs de  en z=h1 et en z= h2. Facile ensuite de déterminer la charge contenue dans le cylindre de base d'aire S entre les altitudes h1 et z compris entre h1 et h2.
en z=h1 et en z= h2. Facile ensuite de déterminer la charge contenue dans le cylindre de base d'aire S entre les altitudes h1 et z compris entre h1 et h2.Merci Vanoise,
Bien reçu, d'accord, ça revient au même !
D'accord aussi pour les questions suivantes,
Bonjour,
Je n'arrive pas à retrouver l'expression de la question 6, j'ai :
Donc d'après le théorème de gauss appliqué à un cylindre entre h1 et z avec h1 < z < h2 on a :
Je n'arrive pas à tomber sur l'expression voulue avec et
. J'ai essayé de rajouter
à droite dans les crochets, c'est ce genre de chose qu'il faut faire ?
Bonjour ferality,
- A la 4ème ligne, ne pas oublier que : Intégrale (-E(h1) ds) = - E(h)*S
- ensuite : Intégrale (t-hm) entre h1 et z = [(z-hm)^2 - (h1 - hm)^2]*1/2
= [(z-hm)^2 - (h2-h1)^2*1/4]*1/2
Je pense que tu as remplacé hm par son expression prématurément. Je reprends ton avant dernière ligne qui est correcte. Petite astuce ( à retenir car souvent utile) : j'ajoute hm2 pour le soustraire aussitôt : cela ne change pas l'expression !
Maintenant : tu peux remplacer hm par sa valeur !
Bonjour ferality,
- A la 4ème ligne, ne pas oublier que : Intégrale (-E(h1) ds) = - E(h)*S
- ensuite : Intégrale (t-hm) entre h1 et z = [(z-hm)^2 - (h1 - hm)^2]*1/2
= [(z-hm)^2 - (h2-h1)^2*1/4]*1/2
Bonjour Chimival,
- Oui j'avais prévu de mettre le +E(h) à droite mais je l'ai oublié, merci.
- Ah bon on a le droit de faire ça ?
ça me paraît un petit peu bizarre car je ne l'ai jamais fait... mais si c'est OK tant mieux ! Merci bien ça me débloque
Je pense que tu as remplacé hm par son expression prématurément. Je reprends ton avant dernière ligne qui est correcte. Petite astuce ( à retenir car souvent utile) : j'ajoute hm2 pour le soustraire aussitôt : cela ne change pas l'expression !
Maintenant : tu peux remplacer hm par sa valeur !
Ca a pris un peu de temps mais j'ai compris ^^ j'imaginais bien qu'il fallait faire une astuce de ce type mais je n'avais pas pensé à faire directement avec
Merci ! Je vais pouvoir avancer sur les autres questions que je posterai si elles me bloquent trop :c
Re-bonjour,
Voici les questions suivantes :
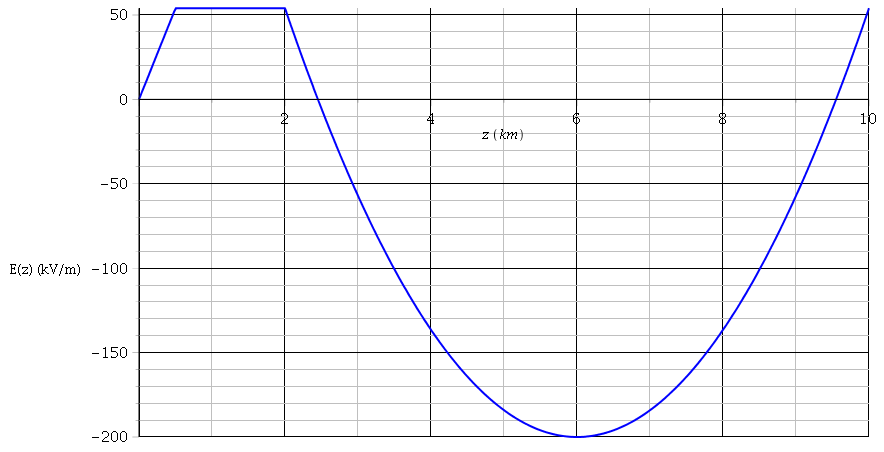
7. Tracer l'allure de E(z) en fonction de l'altitude entre 0 et h2. Expérimentalement on mesure que le maximum du champ électrique dans le nuage est de 200 kV m-1 en valeur absolue. A quelle altitude est obtenu ce maximum ?
8. Déduire des résultats précédents la valeur de ρ0 et la charge totale comprise dans la moitié supérieure du nuage. Commenter.
9. Déterminer le potentiel V(z) sous le nuage (z < h). On supposera que V(0) = 0.
10. Pour que la foudre se déclenche il faut que localement le champ électrique soit de l'ordre de 40 kV cm-1 (champ dit disruptif). Est-ce que les champs considérés jusqu'à présent sont suffisants pour ce déclenchement ?
11. En réalité la foudre se déclenche préférentiellement en présence d'objets pointus. On schématise une pointe par une petite sphère conductrice de rayon R, située à l'altitude z. On considère qu'elle est au potentiel V(z) et qu'elle porte une charge q. Rappeler l'expression du module du champ électrique et du potentiel en fonction de q et r pour r > R. En déduire la relation entre E et V(z) au voisinage de la surface de la sphère.
12. A quelle condition la foudre peut-elle se déclencher ? Déterminer le rayon de la sphère correspondant en fonction de V(z). Faire l'application numérique pour z = 10 m. Comment évolue l'effet de pointe en fonction de l'altitude ?
Je m'interroge sur la 7, je trouve que E(z) présente un minimum en car
et
Aussi et
donc
Et (en remplaçant z par
dans E(z))
Donc coup je trouve que le champ électrique diminue dans le nuage, et je pense que ça n'est pas possible ça :/ Surtout qu'à un moment il devrait être de 200 kV/m et que E(h) vaut 54 kV/m ...
La forme de la fonction que je trouve est en annexe
Tu as effectivement en z=hm un minimum de la valeur algébrique E(z). Cependant, ce minimum de E(z) est une valeur négative : le vecteur champ est alors orienté vers le sol et on peut poser au voisinage de ce minimum : . En z=hm tu as donc un maximum de la norme du vecteur champ et il se trouve numériquement que cette norme est supérieure à la valeur de E(h1).
Tu as effectivement en z=hm un minimum de la valeur algébrique E(z). Cependant, ce minimum de E(z) est une valeur négative : le vecteur champ est alors orienté vers le sol et on peut poser au voisinage de ce minimum :
Je comprend que le champ électrique, à partir de
Je ne comprend pas comment on sait que E(hm) est une valeur négative. Il faudrait pouvoir dire que
Aussi pour avoir un maximum "en norme" en de E(z)
J'ai du mal à saisir cette histoire de norme de E(z). Sur le graphique, nous sommes d'accord que la norme de E(z) est lue sur l'axe des ordonnées ? Plus le point est distant de E=0, plus sa norme est importante ?
Il s'agit des règles habituelles concernant les vecteurs. On pose :
et donc :
E(z) "saute" de manière discontinue dans les E négatifs, non ?
E(z) est nécessairement une fonction continue de z. Seules les distributions surfaciques de charges peuvent créer des discontinuité de vecteur champ.
Plus le point est distant de E=0, plus sa norme est importante ?
Non ! Pour bien comprendre, reprends le théorème de Gauss appliqué au cylindre de hauteur z quelconque, la base d'aire S étant en z=0.
E(z).S=Qint./
 o
o
Imagine que z augmente progressivement à partir de la valeur nulle :
* pour z<h : Qint est positif et augmente linéairement en fonction de z. E(z) augmente linéairement jusqu'à la valeur E(h)=54kV/m
*augmenter z de h à h1 ne fait pas varier E(z) car Qint ne varie pas.
* augmenter z de h1 à hm apporte dans le cylindre de Gauss des charges négatives. La norme du vecteur champ commence par diminuer jusqu'à la valeur nulle puis augmente, le vecteur champ étant alors orienté vers le sol.
* augmenter z de hm à h2 introduit dans le cylindre de Gauss des charges positives, ce qui inverse le sens de variation de E(z). Le nuage étant globalement électriquement neutre : E(h1)=E(h2)=54kV/m
Je reconnais que cet énoncé est un peu piégeant. Puisque, à la question 7,
 o n'est pas connu, la seule façon d'interpréter ce "maximum" de 200kV/m est de considérer qu'il s'agit d'un maximum de la norme du vecteur champ, donc d'un minimum de E(z).
o n'est pas connu, la seule façon d'interpréter ce "maximum" de 200kV/m est de considérer qu'il s'agit d'un maximum de la norme du vecteur champ, donc d'un minimum de E(z).
Voici l'allure de la courbe E(z) = f(z) :
D'accord merci beaucoup pour ces précisions car j'étais confus, je comprend un peu mieux maintenant.
On considère donc que dans la "première moitié" du nuage on a des charges négatives, et dans la seconde moitié, des charges positives c'est bien ça ? J'imagine que c'est clair d'après le graphe de la fonction car la densité passe de négative à positive en
... cependant "physiquement" je ne vois pas bien ce qu'il se passe, après ça n'est pas très grave pour l'instant.
Pour la 8 je trouve puis j'intègre
entre
et h2 je trouve que la charge totale dans la moitié supérieure du nuage est
Pour la 9 je trouve le potentiel
Pour la 10 "non", le champ est encore trop petit.
D'accord avec ta valeur de  o. A noter que l'ordre de grandeur est le même que pour
o. A noter que l'ordre de grandeur est le même que pour  au sol.
au sol.
L'expression de Q est nécessairement fausse car elle n'est pas homogène : une charge est le produit d'une densité volumique de charge par un volume ! L'expression de Q dépend aussi de S et de (hm-h1).
OK pour 9 et pour 10.
D'accord avec ta valeur de
 o. A noter que l'ordre de grandeur est le même que pour
o. A noter que l'ordre de grandeur est le même que pour  au sol.
au sol.
L'expression de Q est nécessairement fausse car elle n'est pas homogène : une charge est le produit d'une densité volumique de charge par un volume ! L'expression de Q dépend aussi de S et de (hm-h1).
OK pour 9 et pour 10.
Ah oui d'accord c'est vrai donc je fais ça maintenant :
D'accord avec toi. Pense systématiquement à vérifier l'homogénéité des résultats. Cela permet de détecter des erreurs et/ou étourderies.
D'accord avec toi. Pense systématiquement à vérifier l'homogénéité des résultats. Cela permet de détecter des erreurs et/ou étourderies.
Oui c'est vrai désolé je ferai plus attention à l'avenir.
Concernant la 11 avec les pointes j'ai vraiment du mal à comprendre la question... j'ai les relations suivantes :
Pour 11 : on pourrait ressortir le cours sur les conducteurs en équilibre électrostatique et évoquer le théorème de Coulomb. Plus simplement ici, compte tenu des symétries et des invariances, tu peux appliquer le théorème de Gauss. Cela va te conduire au résultat suivant : à l'extérieur de la sphère, le potentiel et le vecteur champ sont identiques à ceux créés par une charge ponctuelle, placée au centre de la sphère et égale à la charge totale portée par la sphère. Pour le résultat final, il suffit de faire tendre r (distance du point M au centre de la sphère) vers R+.
Pour 11 : on pourrait ressortir le cours sur les conducteurs en équilibre électrostatique et évoquer le théorème de Coulomb. Plus simplement ici, compte tenu des symétries et des invariances, tu peux appliquer le théorème de Gauss. Cela va te conduire au résultat suivant : à l'extérieur de la sphère, le potentiel et le vecteur champ sont identiques à ceux créés par une charge ponctuelle, placée au centre de la sphère et égale à la charge totale portée par la sphère. Pour le résultat final, il suffit de faire tendre r (distance du point M au centre de la sphère) vers R+.
On applique Gauss avec une surface étant une sphère centrée sur la sphère de la pointe ?
On applique Gauss avec une surface étant une sphère centrée sur la sphère de la pointe ?
Oui mais seulement pour r>R puis on fait tendre r vers R par valeurs supérieures pour avoir le potentiel V de la sphère et le vecteur champ dans l'air au voisinage immédiat de celle-ci. On va ainsi montrer que, pour un potentiel V donné d'un conducteur, le vecteur champ dans l'air au voisinage immédiat du conducteur possède une norme d'autant plus grande que R est petit. Cela peut se généraliser à un conducteur de forme quelconque porté au potentiel V : la norme du vecteur champ au voisinage immédiat est d'autant plus grande que le rayon de courbure de la surface du conducteur est faible, d'où le pouvoir des pointes...
Bonsoir,
Pour la question 8, je crois que (rho_ zéro) =0,749 * 10^(-9) C/m3 (au lieu de 1,124*10^(-9) C/m3 ;
car E(hm) = - (rho_zéro)*(h2+h1)/(4*epsilon_zéro) +E(h)
et non : - (rho_zéro)*(h2-h1)/(4*epsilon_zéro) +E(h)
avec h1 = 2000m ; h2= 10000m ; E(hm) = -200kV ; et E(h) = +54kV
Bonjour,
Pour la question 11) en reprenant le post de ferality du 13-02 à 14h57 et les indications de Vanoise, je dirai :
E(r) = V(r)/r pour r>R (à l'extérieur de la boule) ;
- Si r tend vers R+, E(r) tend vers V(z)/R ;
-Pour que la foudre se déclenche, il faut que E > E disruptif ;
donc que R < ou = V(z)/R c'est à dire R< ou = (Rho_zéro)*z^2 / (2* epsilon_zéro*E)
Je trouve avec z = 10m et E = 40KV/cm, on a R<ou= 6,3 cm
- Est ce juste ?
- une autre question : normalement, le paratonnerre est relié à la Terre par un conducteur ; le potentiel de la terre est V=0 ; donc V(z) est plutôt le potentiel V(R+) que le potentiel de la boule qui lui est 0, non ?
Dans l'expression de R, il faut prendre  au sol et non
au sol et non  o ; la conversion des kV/cm en V/m a bien été effectuée ?
o ; la conversion des kV/cm en V/m a bien été effectuée ?
L'effet de pointe : si un conducteur est à un potentiel V quelconque, le champ électrique dans l'air au voisinage immédiat du conducteur est d'autant plus grand que le rayon de courbure de la surface est faible.
La pointe du paratonnerre est à une altitude d'une dizaine de mètres voire un peu plus et est maintenue au potentiel nul (potentiel au sol). La différence de potentiels est donc plus forte entre le nuage et la pointe qu'entre le nuage et l'air à la même altitude que la pointe ; donc possibilité plus élevé de "claquage" de l'air entre le nuage et la pointe qu'entre le nuage et le sol. Attention : seules les variations de potentiel ont un sens physique...
Bonjour Vanoise
Merci pour ces explications ;
Il y avait des erreurs en effet dans mes résultats ;
Avec rho_sol = 1*10^(-9) c/M3
z = 10m ; E disruptif = 40kv/cm,
On trouve R <ou = 5,6 mm !
(Je me doutais que R= 6,3 cm était bien gros pour une pointe !)