Inscription / Connexion Nouveau Sujet
applicatio de loi de Jurin
Bonjour!!
Je dois calculer la hauteur d'ascension de l'eau entre deux lames de verre distantes de 3 mm et de longueur 1 m.j'ai appliqué la loi de Jurin mais j'arrive pas à déduire la tension superficielle .C'est tout ce que j'ai dans les données
Bonjour Jany,
trouver l'expression de l'ascension d'un liquide entre deux plaques rectangulaires ne pose aucune difficulté, si dans ton cours on a traité le cas de l'ascension dans un capillaire (tube de diamètre très faible). Il suffit de faire la démonstration en l'adaptant à la géométrie du dispositif.
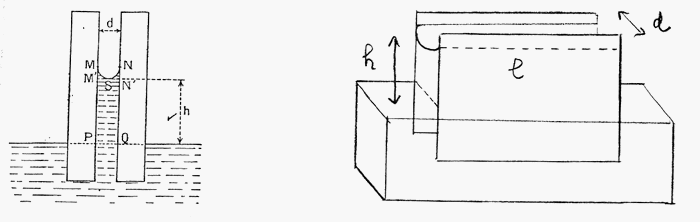
Regarde les figures 1 ci-dessous : j'appelle l la longueur des plaques (1 m ici), d leur écartement (3 mm),  la masse volumique du liquide dans lequel elles trempent,
la masse volumique du liquide dans lequel elles trempent,  la tension superficielle de ce liquide et
la tension superficielle de ce liquide et  son angle de contact avec les plaques.
son angle de contact avec les plaques.
La ligne de contact entre liquide et parois mesure 2l, la résultante verticale des forces ascensionnelles est donc F = 2 l.cos
l.cos .
.
Il y a équilibre lorsque cette force compense le poids du liquide qui s'est élevé d'une hauteur h entre les parois. ce poids s'exprime par mg =  Vg =
Vg =  .dlh.g.
.dlh.g.
On en déduit h = 2 .cos
.cos /(
/( gd).
gd).
Cette expression ne dépend pas de la longueur des plaques (de toutes façons la valeur donnée dans ton énoncé est discutable, car maintenir des plaques de 1 m de longueur à une distance constante de 3 mm l'une de l'autre n'est pas facile à faire...).
Application numérique : si le liquide est de l'eau et que les plaques sont en verre, on trouve facilement dans la littérature  = 0,072 N.m-1,
= 0,072 N.m-1,  = 0° entre l'eau et le verre. En prenant
= 0° entre l'eau et le verre. En prenant  = 1000 kg.m-3, g = 10 m.s-2 et d = 3.10-3 m, on obtient h = 4,8 mm.
= 1000 kg.m-3, g = 10 m.s-2 et d = 3.10-3 m, on obtient h = 4,8 mm.
Une remarque :
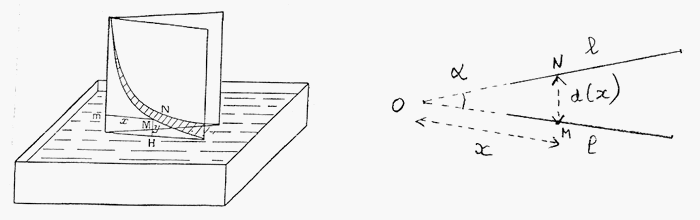
A partir de cet exercice on peut expliquer ce qui se passe si les plaques ne sont plus parallèles, mais font entre elles un angle  (très petit). Regarde les figures 2 :
(très petit). Regarde les figures 2 :
La distance entre les plaques dépend maintenant de la distance x à leur droite d'intersection : d(x) = MN = x (on confond sin
(on confond sin avec
avec  en radians). Le liquide monte alors d'une hauteur exprimée à partir de l'expression précédente, en y remplaçant d par d(x), soit h(x) = 2
en radians). Le liquide monte alors d'une hauteur exprimée à partir de l'expression précédente, en y remplaçant d par d(x), soit h(x) = 2 .cos
.cos /(
/( g
g x) = K/x.
x) = K/x.
La fonction h(x) = K/x est une hyperbole : la ligne de contact entre le liquide et les plaques prend donc cette forme.
Ici à Lille nous avonc mis cette expérience en vidéo, que tu peux voir ici (clique sur la maison) : ![]() .
.
Si tu as des questions n'hésite pas.
c'est exactement ce que j'arrive pas à comprendre,pourquoi considérer la température est égale à O°c par ce que la tension superficielle dépend de cette température
la valeur de la tension superficielle normalement ça change selon la température ,et le degré de la température n'est pas donné alors j'arrive pas de trouver la valeur de cette tension.Merci pour votre explications
La tension superficielle de l'eau vaut 0,073 N/m à 20°C, et 0,076 N/m à 0°C (![]() ). La variation n'est pas tellement grande ! On ne te demande pas de calculer l'ascension entre les plaques au dixième de millimètre, mais d'en donner un ordre de grandeur. J'ai fait l'application numérique avec la valeur de
). La variation n'est pas tellement grande ! On ne te demande pas de calculer l'ascension entre les plaques au dixième de millimètre, mais d'en donner un ordre de grandeur. J'ai fait l'application numérique avec la valeur de  pour 20°C parce que c'est une température plus supportable, mais personne ne t'empêche de refaire cette application pour une autre valeur. Cela dit, tu te noies vraiment dans une goutte d'eau, c'est le cas de le dire...
pour 20°C parce que c'est une température plus supportable, mais personne ne t'empêche de refaire cette application pour une autre valeur. Cela dit, tu te noies vraiment dans une goutte d'eau, c'est le cas de le dire...


