Inscription / Connexion Nouveau Sujet
Analyse dimensionnelle
Bonjour,
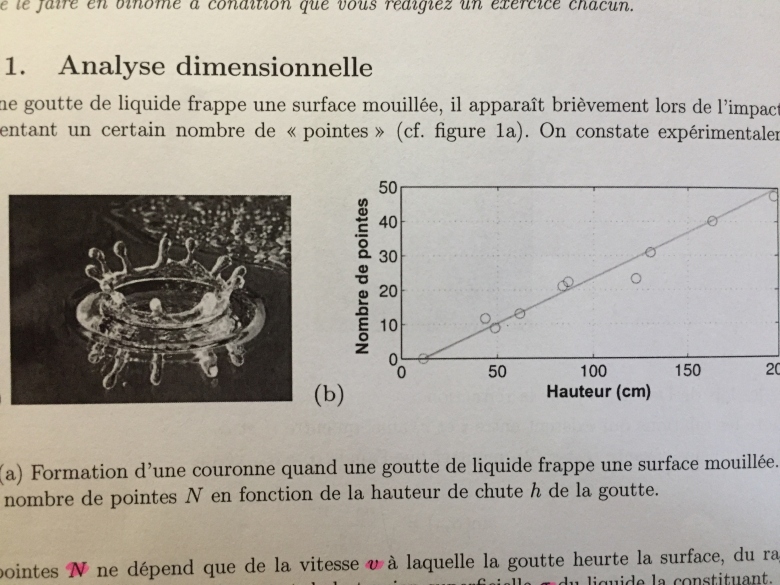
« Quand une goutte de liquide frappe une surface mouillée, il apparaît brièvement lors de l'impact une « couronne » présentant un certain nombre de pointes N. N ne dépend que de la vitesse v à laquelle la goutte heurte la surface, de son rayon r, de sa masse volumique  et de sa tension superficielle
et de sa tension superficielle  .
.
On a N=kvarb c
c d
d
N est un nombre de pointes, donc sans dimension. J'en ait déduit que les exposants sont tous nuls. Sinon l'équation ne serait pas homogène.
Mais en faisant cela l'equation ne veut plus rien dire, parce que N ne dépendrait d'aucune grandeur...
Je viens donc ici pour avoir un petit coup de pouce.
Merci
Bonjour
J'en ait déduit que les exposants sont tous nuls
Pas si simple !
Il faut exprimer chaque grandeur de la formule en fonction des grandeurs fondamentales : masse, longueur, temps et ce sont les exposants qui vont apparaître alors qui seront nuls...
Bonjour à vous deux,
@ Newgatee : ton profil n'est plus à jour : ESPACE MEMBRE / clique sur ton pseudo / MON COMPTE / Mon profil

J'aimerais connaître v (la vitesse de la goutte au moment de l'impact) en faisant une analyse dimensionnelle.
L'énoncé nous dit que les frottements sont négligés. Donc on est dans le vide.
Et d'après Galilée tout corps tombe à la même vitesse dans le vide quelque soit sa masse et sa dimension.
Donc on peut affirmer que la vitesse de la goute au moment de l'impact ne dépend pas de son rayon, ni de sa masse, ni de sa constitution.
Donc si on reprend la formule on a N=kv-2d.
N'ayant pas l'énoncé intégral, je vais peut-être écrire des bêtises... La courbe que tu montre semble indiquer que N est proportionnel à h. Or les lois de la chute libre (frottements négligés sur une hauteur de chute faible) montre que v2 est proportionnel à h.
On peut ainsi poser :
a=2.
La suite est alors facile en tenant compte de ton travail précédent.


