J'ai un exercice à faire dont l'énoncé est le suivant et j'ai mis mes réponses mais je ne sais pas si cela répond bien au problème (les questions sont en bleues) :

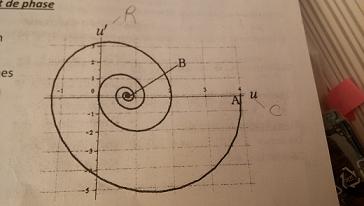
On considère un circuit R,L,C série et on étudie la tension u aux bornes de la capacité  ainsi que la tension u' aux bornes de la résistance. On trace u' en fonction de u et on obtient le graphe ci-contre : (je ne sais pas comment insérer mon graphe : spirale A sur l'axe des abscisses u (4;0) et B(0; pas tout à fait 1)

1) Donner un schéma sur lequel vous figurerez u et u'
On relève des données grâce aux portraits de phases et on obtient EF=B0,8

J'ai fait une courbe allant de 0 à 0,8 (mais je ne sais pas comment mettre sur le site mon graphe)
La représentation peut être assimilée à un portrait de phase car la trajectoire de phase d'un mouvement périodique est une courbe fermée dont le système effectue un tour en période.

2) Déterminer le type de régime observé
Le type de régime observé est un régime pseudo-périodique car l'évolution du système en régime transitoire sont des oscillations décroissantes.

3) Sachant qu'on ferme un interrupteur à t=0, établir que u'(0+)=0. Identifier le point représentant l'état initial et en déduire la condition initiale u(0+)
On sait que la tension pour la résistance est égale :
u'=Ri
pour la capacité on sait que i=Cu

L'état initial est au point A, où u=4V et u'=0V
L'état final est au point B, où u=0,8V et u'=0V
le tracé commence au point A, u(0)=4 et u'(0)=0V
donc pas continuité u'(0)=u'(0+)=0V
De même par continuité u(0)=U(0+)=4V

4) Identifier le point représentant le régime permanent et définir l'état
?

5) Tracer l'allure de u(t)
?


Merci pour votre aide