Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Amplificateur opérationnel

Posté par
azerty4 18-12-18 à 22:59

Bonsoir

une petite question concernant un exercice sur un amplificateur opérationnel

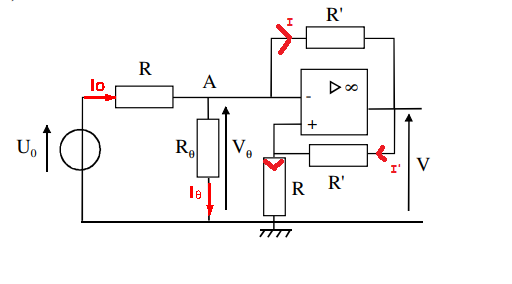
1) On veut Vθ en fonction de R,R', V


J'ai écrit que V+ = V- (contre réaction)

• V ^+ = V^- = V_\theta
• V = (R + R') I' donc I' = \frac{V}{R+R'}
• V = R' I' + V_\theta

En mixant tout ça, je trouve V_\theta = \frac{R}{R+R'} V

On veut ensuite Vθ En fonction de U0, R et Rθ

Si on applique la loi des noeds en terme de potentiel en A, est il correct d'écrire

Avec Vθ = RI' = -RI (relation issu des 4 équation de la question précédente)

\frac{U_0}{R} + \frac{V_\theta }{R_\theta } = I = -I' = \frac{V_\theta }{R} ?


Je bloque vraiment sur cet exercice et je ne suis pas sur de bien applique les théorèmes

Y a til d'autre méthodes (Millman ?) plus simples dans ce types d'exos ?


Merci d'avance !

Bonne soirée

Amplificateur opérationnel

Posté par
vanoisere : Amplificateur opérationnel 18-12-18 à 23:26

Bonsoir

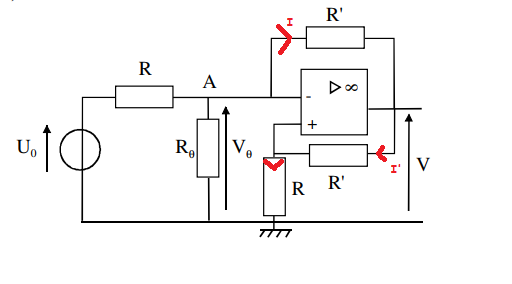
Les résistances R et R' parcourues par le même courant d'intensité I' constituent un diviseur de tension ; on obtient directement le potentiel de l'entrée non inverseuse :

V_{+}=\frac{R}{R+R'}\cdot V

Puisque l'ampli op fonctionne en régime linéaire : V_{+}=V_{\theta} , donc on arrive bien au résultat que tu as obtenu mais de façon plus rapide.

Pour la suite, le théorème de Millman est effectivement particulièrement adapté même s'il est possible de s'en sortir autrement. Mon expérience de jury de concours m'a appris que les autres méthodes sont souvent plus longues et génératrices d'erreurs. Je te fournis ci-dessous un lien sur ce théorème. On obtient ici simplement et directement :

V_{\theta}=\dfrac{\dfrac{Uo}{R}+\dfrac{V}{R'}}{\dfrac{1}{R}+\dfrac{1}{R'}+\dfrac{1}{R_{\theta}}}=\dfrac{R'\cdot Uo+R\cdot V}{R'+R+\dfrac{R\cdot R'}{R_{\theta}}}

Reste alors à tenir compte de la première relation. Je te laisse terminer...

Posté par
azerty4re : Amplificateur opérationnel 18-12-18 à 23:59

Bonsoir,

merci pour votre réponse !

En utilisant Millman je retrouve bien votre résultat

En y insérant V, j'ai un résultat toujours dépendant de R' or cette résistance ne doit plus apparaître

Voyez vous comment supprimer ce paramètre ?

Merci encore,

Bonne soirée

Posté par
vanoisere : Amplificateur opérationnel 19-12-18 à 11:41

En remplaçant dans l'expression déduite du théorème de Millman R.V par (R+R').V, on obtient :

\left(R+R'\right).V_{\theta}+\dfrac{R.R'}{R_{\theta}}\cdot V_{\theta}=R'.U_{o}+\left(R+R'\right).V_{\theta}

Après simplification, R' disparaît :

V_{\theta}=\dfrac{R_{\theta}}{R}\cdot U_{o}

Posté par
azerty4re : Amplificateur opérationnel 19-12-18 à 12:51

merci beacoup !

je m'étais emmêlé dans les simplification de fraction

En essayant de retrouver ce résultat sans Milman (la question nous dit d'utiliser la loi des nœuds en A)  je trouve un résultat différent

• V - V_\theta = - R ' I = R' I' donc I = -I'

• I' = \frac{V_\theta }{R}

Loi des noeuds en terme de potentiel : \frac{U_0}{R} = \frac{V_\theta }{R_\theta } + I
avec les équation précédentes cela donne \frac{U_0}{R} = \frac{V_\theta }{R_\theta } - \frac{V_\theta }{R}

soit V_\theta = U_0 \frac{R_\theta }{R-R_\theta }

je ne vois vraiment pas où est l'erreur

merci d'avance pour votre aide

bonne journée

Posté par
vanoisere : Amplificateur opérationnel 19-12-18 à 13:46

Mais le théorème de Millman n'est rien d'autre que la loi des nœuds avec cependant une petite astuce : pour ne pas s'embrouiller ensuite avec les lois des mailles, on remplace aussitôt chaque intensité par sa valeur déduite de la loi d'Ohm. Illustration pour le point A de ton montage :

I_{o}=I+I_{\theta}

\dfrac{U_{o}-V_{\theta}}{R}=\dfrac{V_{\theta}-V}{R'}+\dfrac{V_{\theta}}{R_{\theta}}

V_{\theta}\cdot\left(\dfrac{1}{R}+\dfrac{1}{R'}+\dfrac{1}{R_{\theta}}\right)=\dfrac{U_{o}}{R}+\dfrac{V}{R'}

On retombe bien sur le résultat fourni par le théorème de Millman et la démonstration est très rapide !

Posté par
vanoisere : Amplificateur opérationnel 19-12-18 à 13:49

J'ai oublié de joindre le schéma sur l'orientation des courants.

Amplificateur opérationnel

Posté par
azerty4re : Amplificateur opérationnel 19-12-18 à 22:20

Merci beaucoup vanoise pour ces explications, c'est beaucoup plus clair pour moi

Nous n'avons quasiment pas abordé le théorème de Millman mais il permet vraiment de simplifier la résolution des problème, en donnant presque automatiquement le résultat

Bonnee soirée


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !