"A1, l'angle que forme la planète P1 avec le soleil"

Cela ne veut rien dire, pour définir un angle, il faut 2 cotés et pas un seul

Même remarque pour "A2, l'angle que forme la planète P2 avec le soleil" ne veut rien dire.

Dit autrement, quelles sont les positions de P1 et de P2 lorsque A1 = 0 et A2 = 0 (partie 1) ?

Rien n'impose dans la partie 1 (à cause des lacunes d'énoncé citées ci-dessus) que si les angles A1 et A2 ont la même valeur (mod 2Pi), les planètes et le Soleil soient alignés.

On faisant comme si l'énoncé étiat correctement rédigé ...



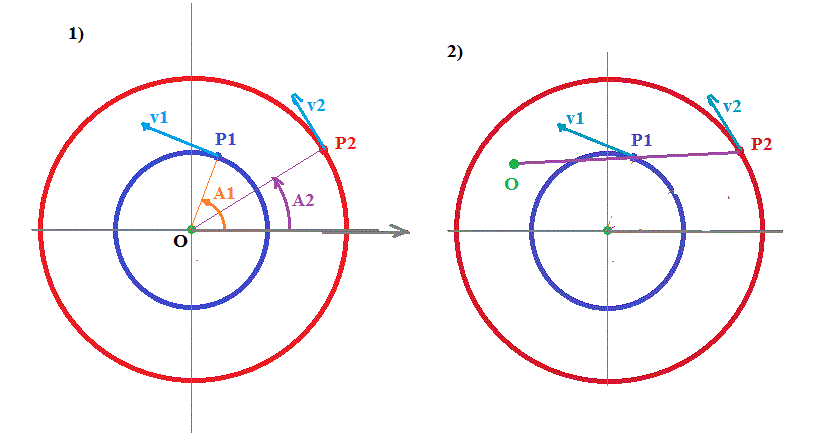
1) (dessin de gauche)
w2 = v2/R2
w1 = v1/R1

En supposant (gratuitement) A1 = A2 = 0 en t = 0 (et les 2 planètes et le Soleil aligné en t = 0)

A1(t) = w1*t
A2(t) = w2*t

A1(t) = (v1/R1)*t
A2(t) = (v2/R2)*t

Il y a alignement lorsque A1(t) = A2(t) + 2.k.Pi (avec k dans Z)

(v1/R1)*t = (v2/R2)*t + k.Pi

t(V1/R1 - V2/R2) = k.Pi

t = k.Pi/(V1/R1 - V2/R2)

Et comme R2 = 2R1 -->

t = k.Pi/(V1/R1 - V2/(2R1))

t = 2k.Pi * R1/(2V1 - V2)

Remarque, les lois de Kepler permettent de calculer le rapport v1 et v2 en fonction de R1 ... mais ce n'est probablement pas attendu dans cet exercice (va savoir ???)
-----
2)
Dessin de droite.

Il faut définir un nouveau repère et ...

Sauf distraction.  

2)



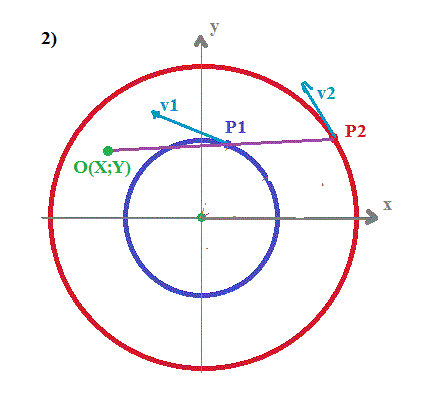
Choix du repère (comme sur le dessin)

O fixe aux coordonnées : O(X ; Y)

Avec P1(x1;y1) et P2(x2;y2) et w1 = v1/R1 et w2 = v2/R2

x1(t) = R1.cos(w1.t)
y1(t) = R1.sin(W1.t)


x2(t) = R2.cos(w2.t)
y2(t) = R2.sin(W2.t)


coeff directeur de la droite OM1 : m1 = (Y - R1.sin(W1.t))/(X - R1.cos(W1.t))
coeff directeur de la droite OM2 : m2 = (Y - R2.sin(W2.t))/(X - R2.cos(W2.t))

O, P1 et P2 sont alignés pour les valeurs de t telle que m1 = m2

--> (Y - R1.sin(W1.t))/(X - R1.cos(W1.t)) = (Y - R2.sin(W2.t))/(X - R2.cos(W2.t))

(Y - R1.sin(W1.t))*(X - R2.cos(W2.t)) = (Y - R2.sin(W2.t))*(X - R1.cos(W1.t))

XY - Y.R2.cos(W2.t) - X.R1.sin(W1.t) + R1.R2.sin(W1.t).cos(W2.t) = XY - Y.R1.cos(W1.t) - X.R2.sin(W2.t) + R1.R2.sin(W2.t).cos(W1.t)

- Y.R2.cos(W2.t) - X.R1.sin(W1.t) + R1.R2.(sin(W1.t).cos(W2.t)-sin(W2.t).cos(W1.t)) =  - Y.R1.cos(W1.t) - X.R2.sin(W2.t)

- Y.R2.cos(W2.t) - X.R1.sin(W1.t) + R1.R2.sin(W1-w2).t)) =  -Y.R1.cos(W1.t) - X.R2.sin(W2.t)

Et avec R2 = 2R1 -->

- 2.Y.R1.cos(W2.t) - X.R1.sin(W1.t) + 2.R1².sin((W1-w2).t)) =  -Y.R1.cos(W1.t) - 2X.R1.sin(W2.t)

- 2.Y.cos(W2.t) - X.sin(W1.t) + 2.R1.sin((W1-w2).t)) =  -Y.cos(W1.t) - 2X.sin(W2.t)

2.R1.sin((W1-w2).t)) + X.(2.sin(W2.t) - sin(w1.t)) - Y.(2.cos(W2.t) - cos(W1.t)) = 0

C'est une équation fonctionnelle donnant les valeurs de t pour lesquelles l'observateur et les 2 planètes sont alignés.

(Et dans le cas particulier où X=Y=0 (Observateur au Soleil), on trouve :

2.R1.sin((W1-w2).t)) = 0

sin((W1-w2).t)) = 0 --> (w1-w2).t = k.Pi

t = k.Pi/(w1 - w2) = k.Pi/(v1/R1 - v2/(2R1))

t = k.Pi.R1/(v1 - v2/2) = 2.k.Pi.R1/(2V1 - V2) ... on retrouve bien la réponse du cas 1.
----------
Pour nénéraliser au cas où l'observateur n'est pas fixé (tourne autour de l'étoile).

Il suffit de donner les coordonnées de l'observateur sous la forme :

x3(t) = R3.cos(w3.t)
y3(t) = R2.sin(W3.t)

et de procéder de manière analogue au cas ci-dessus.

C'est un peu plus long mais sans vraies difficultés.

Essaie ...
-----
Sauf distraction (rien relu).