Merci d'avance

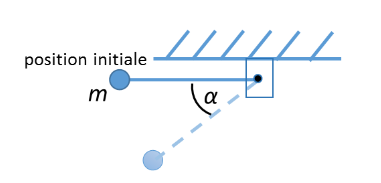
Considère que la bille est soumise à son poids, égal à mg, qui peut être décomposé en un force normale créant la tension du fil et une force tangentielle causant l'accélération de la bille et égale à  mg cos .

Désolé mais je ne vois toujours pas comment on peut trouver

Salut,

En theta = 0 ... il est évident que l'accélération est g.

En theta = 0,

La réponse (a) --> a = 0 (pas bon)
La réponse (b) --> a = g (peut être bon)
La réponse (c) --> a = 2g (pas bon)
La réponse (d) --> a = 2g (pas bon)

Donc la seule réponse possible parmi celles présentées est la réponse b.

C'est forcément la réponse attendue, puisque on la demande sans calculs (du moins sans démonstration nécessitant des calculs un peu élaborés).

Rien n'empêche de tenter de le démontrer ... mais ce n'est clairement pas demandé et devrait même être sanctionné si la démo figure dans la réponse puisque cela ne respecterait pas une consigne de l'énoncé "Y répondre sans calcul".

Sauf distraction.  

Démo (à ne pas faire)

Composante du poids tangentielle à la trajectoire : T = P.cos(alpha)

Et avec aT l'éccélération tangentielle, on a  :  T = m.aT ---> aT = g.cos(alpha)
-----
Delta h entre départ et mobile à l'angle alpha : h = L.sin(alpha) (avec L la longueur de la ficelle)

avec mgh = 1/2.m.v² --> m.g.L.sin(alpha) = 1/2.m.v²

v² = 2.g.L.sin(alpha)

L'accélération centripète est donc aC = v²/L =  2.g.sin(alpha)
-----
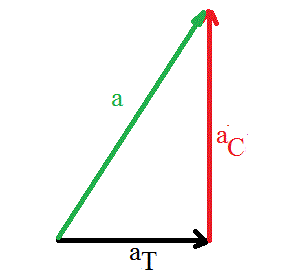
L'accélération (totale) est donc a = RCarrée(aT² + aC²)

a = RCarrée(g².cos²(alpha) + 4g².sin²(alpha))

a = g.RCarrée(cos²(alpha) + 4.sin²(alpha))

a = g.RCarrée(1 - sin²(alpha) + 4.sin²(alpha))

a = g.RCarrée(1 + 3.sin²(alpha))

Sauf distraction.  

Merci beaucoup J-P

En effet je savais pourquoi c'était la réponse (b) mais ce que je voulais savoir c'était comment démontrer cela (juste pour moi et non pour répondre au QCM).

Mais donc pour l'accélération centrifuge, la tension du fil ne rentre pas en compte ?

Et d'où vient ta formule : ??

J'aurais dit que c'était :

En attente d'une réponse

L'accélération tangentielle et l'accélération centripète sont perpendiculaires ... et donc leur résultante se calcule par

Mais je ne comprends pas.



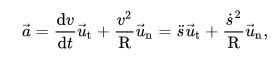
Source :

J'ai toujours appris que comme le montre la capture d'écran ci-dessus.







Source :

Mais un autre site confirme ce que vous venez de me dire, comme le montre l'image ci-dessus, soit :



Donc dans quel cas utilise-t-on la 1^ère formule, dans quel cas la 2^nd ?

Merci d'avance

On a la relation vectirielle :  

et comme et sont orhogonaux, on a (Pythagore) :

et donc

Merci beaucoup !!! C'est très clair maintenant !