Accélération et Freinage - Forum physique - chimie école ingénieur Physique - 318475 - 318475

1 2 +
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:25
Par simple raisonnement dimensionnel vous devez avoir un  au numérateur et un L au dénominateur.
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:27
Vous avez une fonction linéaire pendant le freinage, il suffit d'appliquer la définition du maxi.
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:27
J'en ai très peu fait de raisonnement dimensionnel...
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:28
gts2 @ 26-09-2020 à 08:27

Vous avez une fonction linéaire pendant le freinage, il suffit d'appliquer la définition du maxi.
 Le coefficient contient du cube et du carré
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:31
En quoi le fait que "le coefficient contient du cube et du carré" change le maximum de la fonction puisque ce coefficient est constant.
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:33
Oui c'est vrai mais ça me genait. Et comme la fonction c'est de la forme -bx alors le maximum est en t=0.
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:35
Si bien évidemment on considère que la fonction est défini sur [0;+[ car un temps est toujours positif.
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:38
Je reconnais que le texte est là encore imprécis, mais le maxi est à considérer en norme.



"car un temps est toujours positif." Il n'y aucune raison, pourquoi pensez-vous cela ?



Par contre dans le cas présent 0<t<tf
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:40
On m'a dit qu'un temps est toujours positif...
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:41
C'est à dire en norme ? On n'est pas dans un repère
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:45
L'accélération est un vecteur qui a bien une norme.
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:46
ok. Mais pour l'accélération linéaire son maximum vaut 0 du coup je vois pas comment on peut aller plus loin.
 Posté par 
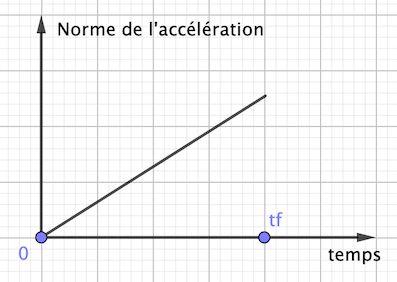
gts2re : Accélération et Freinage   26-09-20 à 08:46
Citation :
On m'a dit qu'un temps est toujours positif...

???
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:48
Un dessin vaut mieux qu'un long discours



 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:50
Le coeff est négatif
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:52
Et je vois pas comment on peut savoir le maximum à tf
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:56
J'ai tracé 



On "voit" le maximum, je ne vois pas ce qu'on peut faire de plus.
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 08:56
Je m'absente pour la matinée...
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:59
gts2 @ 26-09-2020 à 08:56

J'ai tracé 



On "voit" le maximum, je ne vois pas ce qu'on peut faire de plus.
 Bah on n'a pas quelque chose de concret. Enfin quand on me demande ce que vaut l'accélération maximale pour L = 10m et vo=30km.h-1 je sais pas si je peux juster changer les valeurs L et vo. 
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 08:59
gts2 @ 26-09-2020 à 08:56

Je m'absente pour la matinée...
 OK. C'est pas grave. Je sais de toute façon que je vais louper cette matière aux exams mais j'essaye. Et merci de m'aider.
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 13:37
"Je sais de toute façon que je vais louper cette matière aux exams mais j'essaye."



Votre problème est peut-être dans "on n'a pas quelque chose de concret."

C'est tout ce qu'il y a de plus concret : vous êtes sur votre vélo, vous augmentez progressivement votre effort sur les freins, donc le freinage sera maximum lorsque vous allez vous arrêtez, il n'y a pas à chercher le maximum d'une fonction, à chercher la dérivée nulle ou je ne sais trop quoi.
 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 13:40
Citation :
quand on me demande ce que vaut l'accélération maximale pour L = 10m et vo=30km.h-1 je sais pas si je peux juste changer les valeurs L et vo.


Vous avez précédemment effectuer un calcul littéral, donc vrai quelque soit les valeurs de v0 et L. Il s'agit simplement d'une application numérique, dans laquelle on remplace les "lettres" par leur "valeur". 
 Posté par 
IamMere : Accélération et Freinage   26-09-20 à 16:09
Pour l'accélération linéaire :

avec vo = 30km.h-1 et L = 10m



l'accélération maximale = 



avec vo = 50km.h-1 et L = 10m :

 Posté par 
gts2re : Accélération et Freinage   26-09-20 à 16:28
Il faut terminer les calculs : si on fait une application numérique, on veut une valeur numérique (avec une unité).



Deux règles de base :

- un résultat littéral doit être donné en fonction des données et simplifié au maximum

- un résultat numérique doit être donné sous forme numérique (sic!)
 Posté par 
IamMere : Accélération et Freinage   27-09-20 à 07:37
Mais on ne sait pas quand est tf
 Posté par 
gts2re : Accélération et Freinage   27-09-20 à 09:40
Vous avez écrit vous-même le  25-09-20 à 15:51



Citation :
 
 Posté par 
IamMere : Accélération et Freinage   27-09-20 à 14:41
C'est pas gênant de faire avec ça ? J'avais un doute
 Posté par 
gts2re : Accélération et Freinage   27-09-20 à 14:49
Où est le problème ? Vous avez résolu un problème : freinage avec accélération linéaire, et vous utilisez ensuite les résultats.
  Posté par 
IamMere : Accélération et Freinage   27-09-20 à 14:52
d'accord merci.