Inscription / Connexion Nouveau Sujet
accélération
Bonjour,
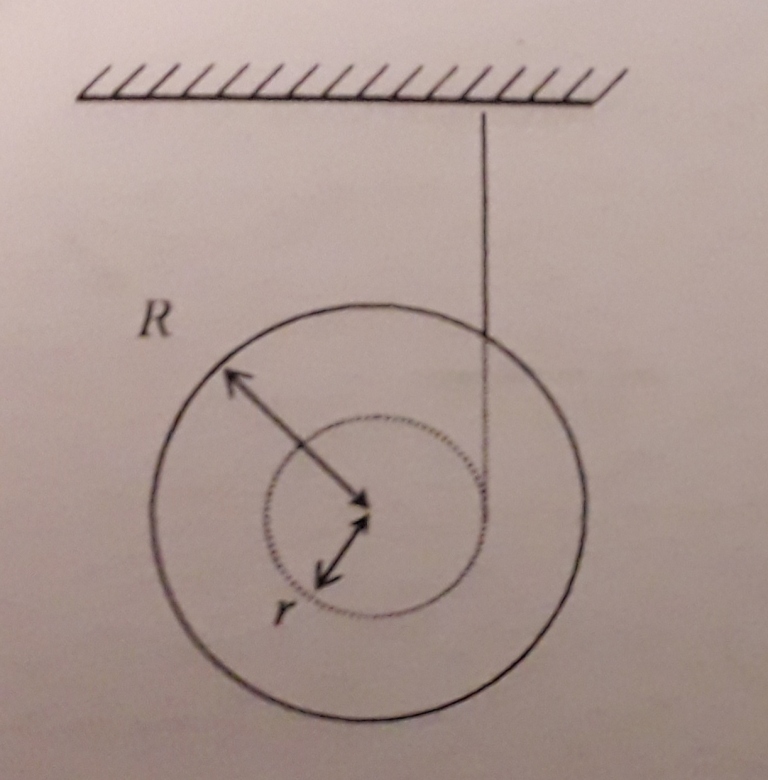
Une bobine se compose de deux disques pleins identiques de masses M et de rayons R enfilés sur un axe de rayon r et de masse négligeable. Le fil entourant l'axe est attaché au plafond. Initialement le fil est vertical et tendu. Déterminer l'accélération verticale de la bobine.
La première image est celle de l'énoncé et la deuxième de l'aide.
La solution: a=g/[1+(R2/2r2)]
PFD: ma=2Mg-T
Ici m=2M donc 2Ma=2Mg-T
Ensuite je suis perdu, je me demande s'il faut utiliser le moment des forces M=r^T
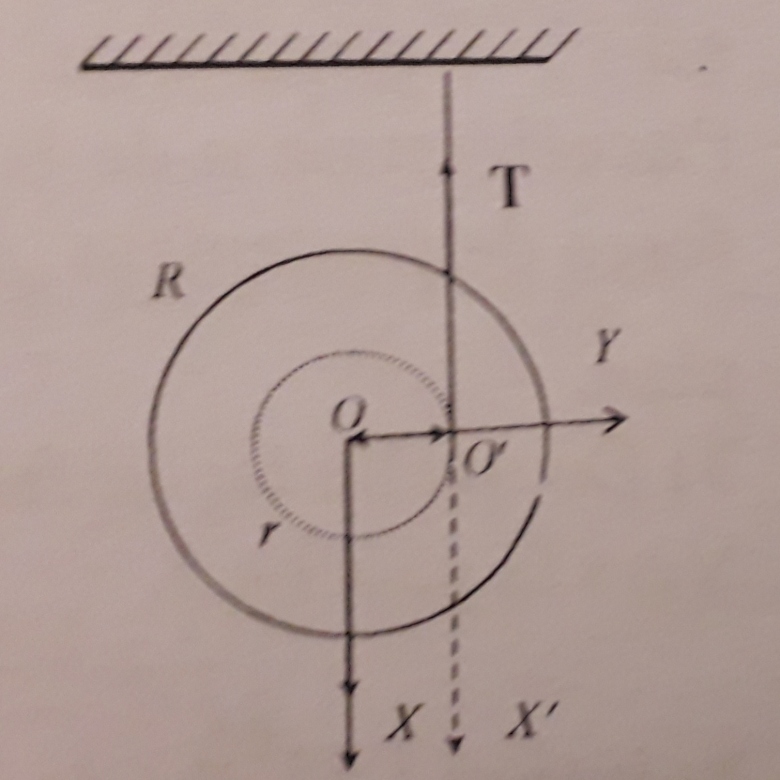
Moment de force M1=r(OO')^T, en z ça donne -T et M2=r(O)^2Mg, en z ca donne -2Mg.
I*
(accélération angulaire)=M1+M2
Bonsoir
S'il s'agit du moment en O des forces s'exerçant sur la bobine, exprimé dans (O,X,Y,Z), c'est pas vraiment ca
Oups, je me suis trompé, on s'intéresse en x pas en z.
Oui, il s'agit du moment en O des forces s'exerçant sur la bobine, exprimé dans (O,X,Y,Z)
r(O)^2Mg= 0(en x)
r(OO')^T=r (en x)
J'ai du mal avec tes notations
M(T/o) = Tr ez
Et le moment/O du poids est nul puisqu'il sapplique en O
ezétant le vecteur directeur unitaire de Oz
Annuler
connectez vous