Niveau maths spé

A.O en régime linéaire

Posté par
redoine93 01-03-16 à 20:19

Bonsoir,

Les amplificateur ne sont pas un objectif du programme, mais je souhaite quand même travailler dessus. C'est pourquoi, je me suis lancé dans un exercice il y a peu de temps.
L'énoncé est donné ci-dessous :

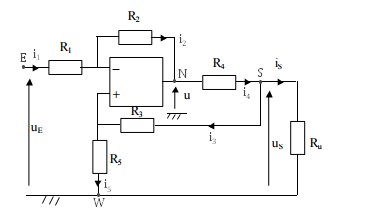
Considérons le circuit attachée.
Il s'agit ici de calculer la tension $u$ en fonction de $u_S$ $u_E$ et des résistances.
On suppose que l'amplificateur est idéal, et on se place en régime linéaire.

Voici ce que j'ai fait :

je noterai $u_k$ la tension aux bornes de la résistance $R_k$ en convention récepteur.

J'ai fait une loi des nœuds :
$i_1 = i_2 = i_3+i_S = i_5+i_S = i_4$
Soit :
$\frac{u_E}{R_1} = \frac{u_2}{R_2} = \frac{u_3}{R_3} + \frac{u_S}{R_u} = \frac{u_5}{R_5} + \frac{u_S}{R_u} = \frac{u_4}{R_4}$

Puis une loi des mailles :
$u_S = u_3 + u_5$
$u_S + u_1 + u_2 + u_4 = 0$

Mais je n'arrive pas à faire apparaître la tension $u$
Je sais qu'elle correspond visiblement au potentiel $V_N$ du nœud $N$
Mais rien n'y fait, j'ai essayé pas mal de choses pourtant.

Je précise que j'ai remarqué que $R_1$ , $R_2$ et $R_4$ sont en série
Tout comme $R_5$ et $R_3$ qui sont en série, mais en dérivation par rapport à $R_u$

Aussi, j'ai remarqué que :
$u_2 = -V_N$
$u_1 = V_E$
$u_4 = V_N - V_S$
$u_S = V_S - V_W$

Mais même avec ces éléments, les lois des mailles et des nœuds que j'ai établi ne m'aident pas.
Quelqu'un aurait une idée ?
Merci d'avance

A.O en régime linéaire

Posté par re : A.O en régime linéaire 01-03-16 à 23:18

Oups, j'y suis parti un peu vite.
Je pensais que les potentiels $V_{+}$ et $V_{-}$ était nul pour un ampli idéal.
Mais pas du tout, j'avais vu ça quelque part, car c'était relié à la masse, et j'ai généralisé ça, j'ai un peu honte... Du coup, ce que j'ai fait est faux, archi faux même.

Donc je me rattrape, je tente de faire usage du théorème de Millman.
On a :

$V_{+} = \frac{\frac{V_S}{R_3} + \frac{V_W}{R_5}}{\frac{1}{R_3}+\frac{1}{R_5}}$
$V_{-} = \frac{\frac{V_E}{R_1} + \frac{V_N}{R_2}}{\frac{1}{R_1}+\frac{1}{R_2}}$

Or dans l'hypothèse de l'A.O idéal nous avons :
$V_{+} = V_{-}$

Et puisque $V_W = 0$

Donc :

$\frac{\frac{V_S}{R_3} }{\frac{1}{R_3}+\frac{1}{R_5}} = \frac{\frac{V_E}{R_1} + \frac{V_N}{R_2}}{\frac{1}{R_1}+\frac{1}{R_2}}$

Il en résulte que :

$V_N = \frac{R_5}{R_1}\frac{R_2+R_1}{R_3+R_5}V_S - \frac{R_2}{R_1}V_E$

En observant le circuit on remarque que :
$V_N = u$
$V_S = u_S$
$V_E = u_E$

D'où l'expression :
$u = \frac{R_5}{R_1}\frac{R_2+R_1}{R_3+R_5}u_S - \frac{R_2}{R_1}u_E$

J'ai un peu triché en utilisant ce théorème hors programme, bon, demain je posterai la résolution avec la loi des nœuds appliquée sur les potentiels.

Posté par re : A.O en régime linéaire 02-03-16 à 10:59

i1 = i2 = (Ue-U)/(R1+R2)
V- = Ue - R1*i1
V- = Ue - R1.(Ue-U)/(R1+R2)

V+ = Us*R5/(R3+R5)

Et si l'ampli travaille dans sa zone linéaire (ce qui n'est pas forcément le cas en fonction des valeurs des différentes résistances), alors :

V- = V+ et donc : Us*R5/(R3+R5) = Ue - R1.(Ue-U)/(R1+R2)

Us*R5*(R1+R2) = Ue*(R1+R2).(R3+R5) - R1.(Ue-U)*(R3+R5)

Us*R5*(R1+R2) = Ue*R2.(R3+R5) + U*R1*(R3+R5)

U = Us * (R5/R1) * (R1+R2)/(R3+R5) - Ue*R2/R1

Sauf distraction.

Posté par re : A.O en régime linéaire 02-03-16 à 17:00

Merci beaucoup,
Je n'avais pas pensé à utiliser des diviseurs de tensions.
Pourtant, j'avais bien repéré les résistances en série

Cdt.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

A.O en régime linéaire

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique