Inscription / Connexion Nouveau Sujet
Voiture et Piéton
Bonjour, pouvez-vous m'aider s'il vous plaît ;
Soit une voiture de largeur L en mouvement le long d'un trottoir rectiligne x' x. Un piéton décide de traverser la route au moment où la voiture se trouve à une distance D.
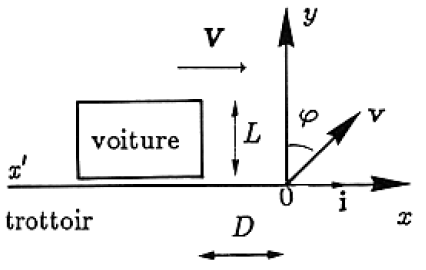
Le mouvement du piéton est rectiligne, uniforme, de vitesse 
, incliné d'un angle 
par rapport à l'axe Oy. La voiture se déplace à la vitesse constante V = V 
.
Quelle doit être la valeur de 
étant minimum (on précisera la valeur vmin) ?
Bonsoir,
Quelle doit être la valeur de étant minimum (on précisera la valeur vmin) ?
Il manque quelque chose...C'est incompréhensible
Quelle doit être la valeur de afin que la collision avec la voiture soit évitée, le module v de étant minimum (on précisera la valeur de vmin) ?
Il faut établir les équations du mouvement.
Pour la voiture :
xV = V t - D
yV = L (pour le bord le plus éloigné du bord)
Pour le piéton :
xP = v sin t
yP = v cos t
La position limite pour éviter la collision est
xP = xV
yP = yV
v sin t = V t - D
v cos t = L ==> t = L / v cos
Et on remplace la valeur de t dans la première équation
Annuler
connectez vous