Inscription / Connexion Nouveau Sujet
vitesse et deplacement
bonjour,
je sollicite une fois de plus votre aide car je bute sur certains exercices.
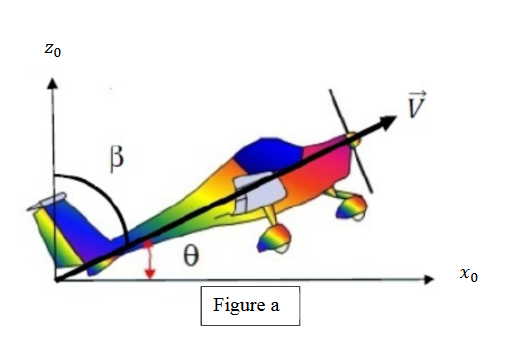
On dit qu'un avion vole en montée stabilisée lorsque sa vitesse est constante et sa trajectoire montante rectiligne. La figure a représente le vecteur vitesse , de norme v ܸd'un avion en montée stabilisée. Sa trajectoire fait un angle
 avec le sol horizontal et un angle
avec le sol horizontal et un angle  avec la verticale.
avec la verticale.
Déterminer la vitesse au sol et la vitesse ascensionnelle de cet avion en fonction de (V; ) puis en fonction de (V;
) puis en fonction de (V; )
)
voir figure a
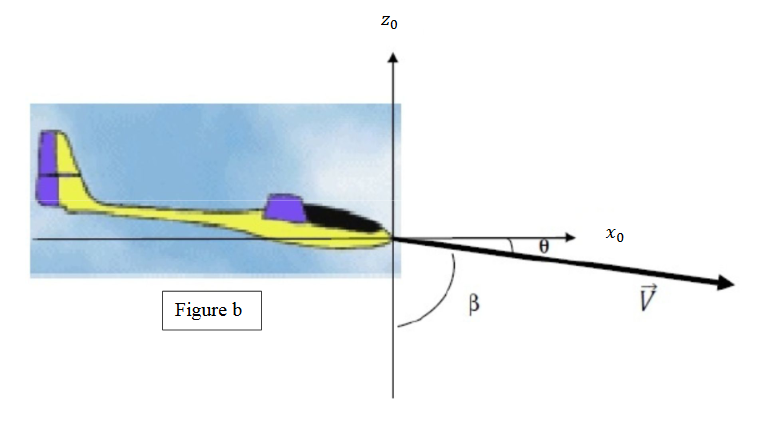
La fig ure b représente cette fois-ci un avion en descente stabilisée (vitesse constante, trajectoire rectiligne descendante). Déterminer à nouveau la vitesse au sol et la vitesse ascensionnelle de cet avion en fonction de (V; ) puis en fonction de (V;
) puis en fonction de (V; )
)
voila ce que j'ai fait
figure a
en fonction de (V; )
)
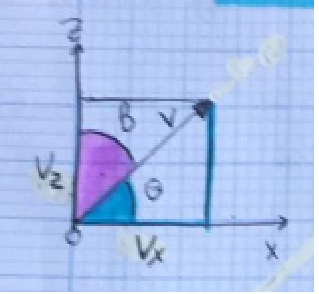
vitesse ascenscionelle:
: cos
 .Vx
.Vx
sin .Vz
.Vz
| |=
vitesse au sol
ici je bute, je presume qu'il faut faire la meme chose mais selon x et y?
merci a tous
Bonjour,
Il faudrait déjà éclaircir le texte : que veut dire "vitesse au sol" ? En cherchant dans le vocabulaire aéronautique, on voit que vitesse-sol est la composante horizontale de la vitesse de l'avion, c'est donc la composante de la vitesse selon x.
Ensuite la vitesse ascensionnelle, quand on fait une ascension, on monte, c'est donc la composante de la vitesse selon z.
desolé je suis trop bete, pas de composante en y, la vitesse au sol ne depend que de x en fait
dnc pour la vitesse au sol on a juste v=vx non?
bonjour,
c'est un exercice que j'ai recopier tel quel, je n'ai pas plus de details.
mais je pense egalement que c'est ca, donc pour la vitesse au sol, on prend juste x
mais pour la vitesse ascenscionnelle, on prend juste selon l'axe z ou on prend egalement l'axe x?
j'ai regarder aussi la definition de vitesse ascensionnelle,
La vitesse ascensionnelle (Va) est la vitesse à laquelle le traileur se déplace d'un point bas A à un point B situé plus en hauteur : Va = dénivelé positif réalisé / 1h
donc pour la vitesse ascencionnelle on a bien ce que j'ai ecrit dans le premier post, et pour la vitesse au sol on a:
\vec{V} = Vx
c'est bien ca?
j'ai verifier sur un site d'aeronautique aussi du coup et effectivement la vit ascensionelle ne depend que de z, et la vitesse au sol que de x, du coup le module de v vaut la racinne carré de la somme des carrés des deux vitesse
donc on a vit asc selon  : sin
: sin .Vz
.Vz
selon  : cos
: cos  .Vz
.Vz
vit au sol
cos .Vx
.Vx
sin .Vx
.Vx
la je pense que c'est bon?
je viens de me rendre compte du gros n'importe quoi, je suis sur plusieurs exercice en meme temps et je me suis embrouillé tout seul, et j'ai pas mis le temps, ben bravo !
Vx c'est la vitesse selon x et Vz la vit selon z
donc vit au sol = Vx et vit asc = Vz
donc pour Vx selon  on a (cos
on a (cos )/t et selon
)/t et selon  sin
sin /t
/t
pour Vz on a sin /t cos
/t cos /t
/t
"Vx est la distance parcourue en x" : ce n'est donc pas une vitesse.
Supposons que Vx soit la composante de la vitesse selon x, on a alors en effet (17:25) vitesse-sol = Vx.
Pourquoi à 17:47 se retrouve -t-on avec "vit au sol : cos  .Vx ?
.Vx ?
Il faut éclaircir vos notations, je propose :
Vx : composante de la vitesse selon x
Vy : composante de la vitesse selon y
: vecteur vitesse.
V : norme de
1- Quelle est la relation entre (Vx,Vy,) puis (V,Vx,Vy) ?
Puis une fois ceci éclairci, répondre à la question du texte.
oui desolé c'est ce que j'ai marqué juste au dessus, je me suis eparpillé sur mes exercice et je me suis embrouillé tout seul dans mes notations
donc avec 0 et
0 vecteur unitaire:
= Vx.
0 + Vy.
0
v=
jusque la ca va?
ok cool
donc maintenant je cherche Vx en fonction de V et  pour repondre a la question.
pour repondre a la question.
mais je seche un peu du coup, d'apres l'equation du dessus
Vx. 0=
- Vy.
0
donc Vx² = V²-Vy²
je ne vois pas comment j'incorpore  ou
ou  quelque part
quelque part
je sais que x = Vx.t donc Vx= x/t avec t le temps
ici x en fonction de  et
et 
j'ai x= cos =sin
=sin
je suis pas sur d'aller dans le bon sens avec tout ca
Ce n'est pas un problème d'équation, c'est un problème de géométrie : il faut lire le dessin traduisant , dessin sur lequel vous aurez reporté les angles.
En fait vous y avez déjà répondu mais avec un tel meli-melo de notation que c'était illisible.
x ne peut être égal à cos  : x est une longueur et le cosinus est sans dimension.
: x est une longueur et le cosinus est sans dimension.
D'autre part on ne connait pas x mais V
desolé je voulais faire un apercu c'est un vecteur entre les barres
donc je disais
Vx= |||| cos

Vy= |||| sin

ha oui desolé,
Vx = Vcos
Vy = Vsin
Vx=Vsin
Vy= Vcos
Pour la descente
Vx = V cos
Vy = V sin 
Vx = -Vsin
Vy= Vcos
Pour la descente je ne suis pas sur des signes
Je suppose que vos y sont des z ?
Je suppose d'autre part les angles non orientés donc entre 0 et  /2.
/2.
Pour l'avion OK
Pour le planeur, il se dirige manifestement dans le sens des x positifs et il descend donc ?
oui il descend desolé j'ai zappé, j'etait surtout sur le signe des sinus et cos donc en z negatif du coup :
Vx = V cos
Vy = -V sin
Vx = -Vsin
Vy= -Vcos
par contre pour Vx = -Vsin j'ai un moins par rapport au sens du sinus, c'est correct?
j'ai un moins par rapport au sens du sinus, c'est correct?
D'après votre dessin, les angles ne sont pas orientés, donc s'il y a un + pour Vx, il sera là pour les deux expressions.