Inscription / Connexion Nouveau Sujet
Vitesse
Bonjour,
Un skieur de masse m=80kg dévale une piste de longueur L=500m, cette piste fait un angle de 20 degrés avec l'horizontale, l'altitude en bas est de 1000m. Le skieur descend la piste sans vitesse initiale, quelle est sa vitesse en bas de la piste ?
Je néglige les forces de frottements. Le point A se situe en haut de la piste et le point B en bas.
•J'utilise la conservation de l'énergie mécanique:
Em(A)=Em(B)
Ec(A)+Epp(A)=Ec(B)+Epp(B)
Ec(A)=0 car le skieur n'a pas de vitesse initiale
mgz(A)=mv(B)2/2 +mgz(B)
zA=zB+Lsin
v(B)=(2gLsin )1/2
)1/2
•En utilisant le théorème de l'énergie cinétique  WFext=
WFext= Ec :
Ec :
Ec(B)-Ec(A)=W(P)+W(R)
Ec(A)=0 car le skieur n'a pas de vitesse initiale
W(R)=0 car P ne travaille pas (R et le vecteur de déplacement sont orthogonaux entre eux; R est perpendiculaire à la piste)
mv(B)2/2 = mgLcos
v(B)=(2gLcos )
)
Pourquoi est-ce que je trouve un résultat différent avec les deux méthodes ?
Merci d'avance
bonjour
Je n'ai pas sous les yeux le schéma qui t'a servi dans ton raisonnement mais il est probable que le travail du poids par le seconde méthode fasse intervenir le cosinus du complémentaire de  donc sin(
donc sin( ).
).
A vérifier...
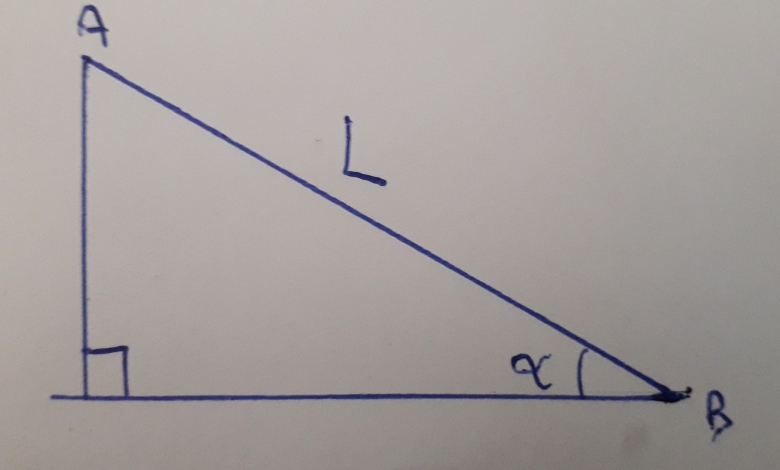
J'ai fait ce schéma
Je crois que je viens de m'apercevoir de l'erreur. Pour le théoreme de l'énerfie cinétique je dois prendre cos(90- )=sin
)=sin et non juste
et non juste