Inscription / Connexion Nouveau Sujet
viseur dioptrique
Bonjour,
J'ai une question sur un exercice d'optique.
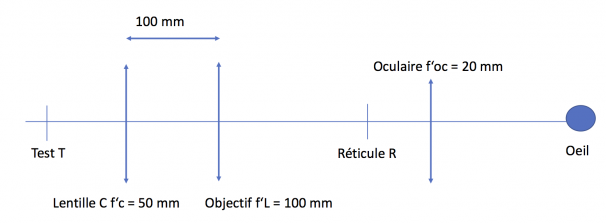
On étudie un viseur dioptrique dont je joints un schéma de principe dans mon post. Dans ce système, le viseur permet d'effectuer la mise au point sur un objet qui peut être à l'infini ou à distance finie, en jouant sur la distance objectif-oculaire. Cette distance est variable. La lentille et le test T mobile placés en amont du dispositif permettent de réaliser la calibration.
Si le viseur est réglé sur l'infini alors F'obj=Foc (obj + oc = doublet afocal).
On s'intéresse au cas où la mise au point s'effectue à 200 mm en avant de l'objectif (donc l'ensemble objectif-oculaire n'est plus afocal).
a) Dans quel sens et de quelle distance faut-il déplacer l'oculaire ?
b) Dans quel sens et de quelle distance faut-il déplacer le test mobile T pour que son image à travers le viseur soit toujours nette ?
c) Quelle sera la dimension de l'image de T dans le plan du réticule R ?
J'essaie d'appliquer les relations de Newton mais j'obtiens des résultats aberrants. J'ai besoin de votre aide.
Merci d'avance
Bonjour
Il faut commencer par bien comprendre que la distance réticule - oculaire est réglée de façon que l'il voit sans fatigue le réticule. Si l'oeil est normal, il voit sans fatigue à l'infini : le réticule doit être placé dans le plan focal objet de l'oculaire.
Ceci étant réglé, l'oeil verra également l'objet visé si l'image de cet objet par l'objectif (ou par l'ensemble objectif - lentille additionnelle) est réelle et se forme dans le plan du réticule.
Une fois ceci bien compris, il suffit de raisonner sur les propriétés de l'objectif...
Je te laisse réfléchir et proposer une solution.
merci pour ta réponse si rapide !
le réticule doit être placé dans le plan focal objet de l'oculaire.
Ce point-là, je l'avais bien compris. Mais c'est le second, que tu as écrit en gras qui me pose problème : en effet, je me suis dis, en regardant simplement mon schéma "Pourquoi devoir bouger l'oculaire si le rayon sortant parallèle à l'axe après avoir traversé le dispositif passe par Foc confondu avec F'L " ? Comme je ne fais bouger que la lentille additionnelle et non l'objectif, je ne comprends pas pourquoi la distance F'L-Foc change...
Cela ne parait pas évident dans la vie courante car l'il accommode automatiquement en fonction de ce que l'on cherche à observer mais l'il ne voit distinctement à un instant donné (donc pour une accommodation donnée) que des objets situés dans un même plan. Si l'oeil voit distinctement le réticule, il ne peut voir en même temps que des images situées dans le plan du réticule.
Sinon, je ne comprends pas bien ton énoncé. La distance objectif - oculaire est réglable : oui mais la distance oculaire - réticule doit rester fixe et cela n'est pas précisé dans ton énoncé.
Autre point que je ne comprends pas bien : la lentille C est -elle présente dès la première question ? Je ne comprends pas bien son rôle...
La lentille C sert à partir de l'étape de mise au point pour un objet qui n'est plus à l'infini (autrement, elle n'est pas présente).
Et oui, le réticule est bien mobile.
Je ne comprends pas : à partir de quelle question faut-il prendre en compte la présence de la lentille C : avant ou après la mise au point à 200mm de l'objectif ? Dans les deux cas, les valeurs numériques me paraissent très étranges...
J'ai en quelque sorte édulcoré l'énoncé de l'exercice, il y avait une première partie (que j'ai évoquée) dans laquelle on ne s'intéressait qu'au viseur réglé sur l'infini. La lentille C intervient donc dès la première question a) puisque j'imagine que c'est elle qui va permettre d'effectuer la mise au point à 200 mm en avant de l'objectif. Comme celui-ci est fixe, je pense que c'est la lentille C qu'il faut bouger de 100 mm vers la gauche, par rapport au dessin que j'ai joint. De fait, je ne comprends pas du tout pourquoi le doublet n'est plus afocal...
Mais en relisant le tout, je me rends compte que la lentille C est déjà présente lors du réglage à l'infini, à une distance 100 mm de l'objectif (comme sur mon schéma).
Mon problème (j'essaie de bien formuler) : je ne vois pas pourquoi il serait nécessaire de déplacer l'oculaire si l'on bouge la lentille C de 100 mm vers la gauche. Car si je place toujours le test mobile au foyer objet de C, le viseur serait toujours réglé sur l'infini !
Ton dernier message prouve que tu as bien compris comment transformer une lunette réglée à l'infini en un viseur à frontale fixe. Cela est bien utile en focométrie de précision.
Je reprends ton message du 30-10-18 à 08:41 selon lequel l'ensemble {lentille C - lunette} permettrait de voir à l'infini.
L'image par C d'un objet à l'infini est dans son plan focal image soit 50mm devant l'objectif. L'objectif doit donner de cette image intermédiaire une image définitive sur le réticule. Or, cela est impossible car la distance image intermédiaire - objectif est inférieure à la distance focale de l'objectif ! Cela est impossible !
Reprends maintenant la figure que tu as fournie. La distance entre T et la lentille C est égale à 100mm soit 2f'c. La lentille C donne de T une image intermédiaire située à 100mm à droite de C soit dans le plan de l'objectif ! Impossible à traiter en assimilant les lentilles à des lentilles minces. Les formules habituelles sur les lentilles minces ne sont valides que si l'épaisseur des lentilles est négligeable devant toutes les distances horizontales du problème : les rayons de courbure des dioptres et les distances lentille objet et lentille - image. Bref : ce problème ne peut pas être traité en assimilant les lentilles à des lentilles minces.
Inutile de me demander ce que je pense de la compétence du concepteur de cet énoncé ! 
Merci pour tes réponses.
J'ai quand même obtenu la correction qui indique les résultats suivants :
"On doit déplacer l'oculaire de 100 mm à droite par rapport à l'objectif donc F'obj Foc = 100 mm. Il faut rapprocher le test T de la lentille C. CT = -33,3 mm."
Si tu pouvais m'expliquer comment on trouve ça, surtout la distance test-centre de la lentille, ça m'aiderait beaucoup 
Pour obtenir ce résultat, il faut dans un premier temps, enlever la lentille C. Suppose la lunette réglée à l'infini : la distance objectif - réticule vaut f'L=100mm. Place alors T devant l'objectif, 200mm devant lui, la lentille C étant toujours absente. La distance de T à l'objectif étant 2f'L, l'image de T par l'objectif se formera à la distance 2f'L=200mm de l'objectif. Pour que T soit vu à travers l'oculaire sur le réticule, il faut déplacer vers la droite l'ensemble {réticule oculaire} de 100mm.
Supposons maintenant que l'on ajoute la lentille C sans toucher au réglage précédent de la lunette. Il faut alors déplacer T de façon que la lentille C donne une image virtuelle de T située à la position antérieure de T soit à 200mm de l'objectif. (C se comporte alors en loupe).
Toutes ces hypothèses ne pouvaient évidemment pas être devinées avant ton dernier message !
D'accord, c'est beaucoup plus clair.
Pour calculer CT, je peux utiliser Descartes : 1/CT' - 1/CT = 1/f'c mais je ne vois pas bien ce que vaut CT'...
En fait (juste pour voir si j'ai bien compris), il faut s'arranger pour que l'ajout de la lentille C située au foyer image de l'objectif donne une image située à 200 mm en amont de l'objectif. On peut donc déjà dire que puisqu'il s'agit d'une image virtuelle, on devra avancer T pour que celui-ci se situe entre le foyer objet de la lentille C et l'objectif.
Néanmoins toutes ces hypothèses sont vraiment bien loin d'être évidentes ! (l'histoire de "j'ajoute C ou pas")
Donc ici, je viens de réaliser, pour faire suite à mon message de 12:30 : j'applique Descartes pour la lentille C. J'ai donc : CT' = -100 mm ce qui donne par application de la formule, CT = -33,3 mm ! Ce que je voulais 
La lunette est réglée pour donner dans le plan du réticule une image nette d'un objet située 200mm devant l'objectif. En présence de C, il faut donc que l'image de T par C soit 200mm devant l'objectif. Pour cela, C doit fonctionner comme une loupe : il faut rapprocher T de C à une distance inférieure à f'C
Si tu note T' l'image de T par C :
avec :
La valeur absolue de représente la nouvelle valeur de la distance de T à C : 33,3mm. Comme prévu, on obtient une valeur inférieure à f'c


